Analyze and sketch a graph of the function .
A)
B)
C)
D)
E)
Use the function to find
A)
B)
C)
D)
E)
Determine the range of the function .
A)
B) [ ]
C)
D) ]
E)
Find the derivative of the following function.
A)
B)
C)
D)
E)
Evaluate the integral
A)
B)
C)
D)
E)
Find the radius of convergence of where .
A) 1
B)
C)
D) 8
E) 16
Use separation of variables to find the general solution of the differential equation.
A)
B)
C)
D)
E)
The revenue R for a company selling x units is . Use differentials to
approximate the change in revenue if sales increase from to units.
A) 28,000 dollars
B) 30,000 dollars
C) 25,000 dollars
D) 33,000 dollars
E) 40,000 dollars
True or False: These three points are collinear.
(1, 3), (0, 2), (“2, 1)
A) True
B) False
Use the error formulas to find n such that the error in the approximation of the definite
integral is less than 0.0001 using the Trapezoidal Rule.
A) 25
B) 26
C) 24
D) 22
E) 23
Test for relative extrema and saddle points.
A) saddle point at
B) saddle point at
C) saddle point at
D) relative minimum at
E) relative minimum at
Find the intercepts of the plane given by .
A) The -intercept is . The -intercept is .
The -intercept is .
The -intercept is .
B) The -intercept is . The -intercept is .
The -intercept is .
The -intercept is .
C) The -intercept is . The -intercept is .
The -intercept is .
The -intercept is .
D) The -intercept is . The -intercept is .
The -intercept is .
The -intercept is .
E) The -intercept is . The -intercept is .
The -intercept is .
The -intercept is .
Determine the relative extrema of the function on the interval
.
A) relative minimum: relative maximum:
B) relative minimum: relative maximum:
C) relative minimum: relative maximum:
D) relative minimum: relative maximum:
E) relative minimum: relative maximum:
The average time between incoming calls at a switchboard is 3 minutes. If a call has
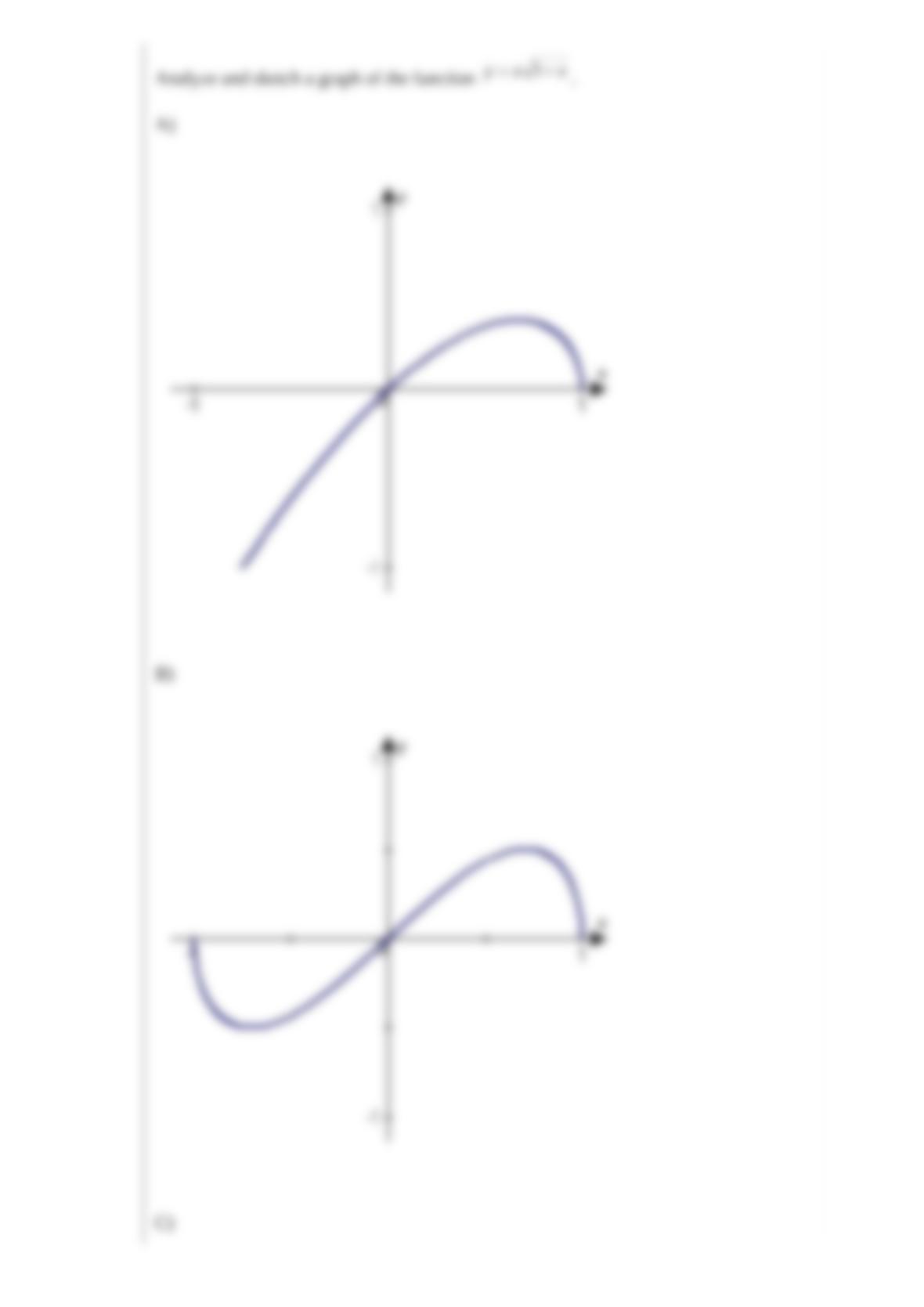
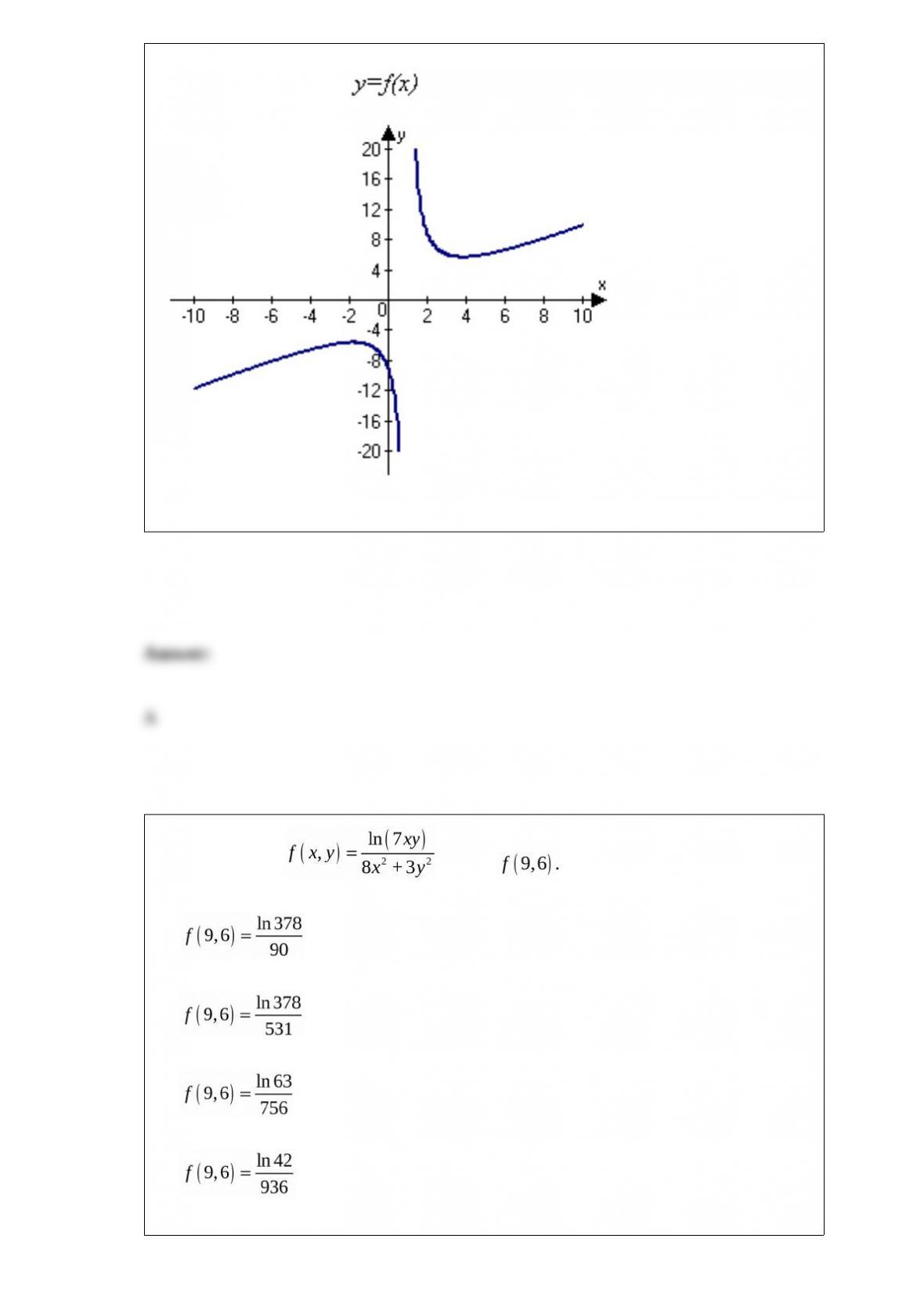
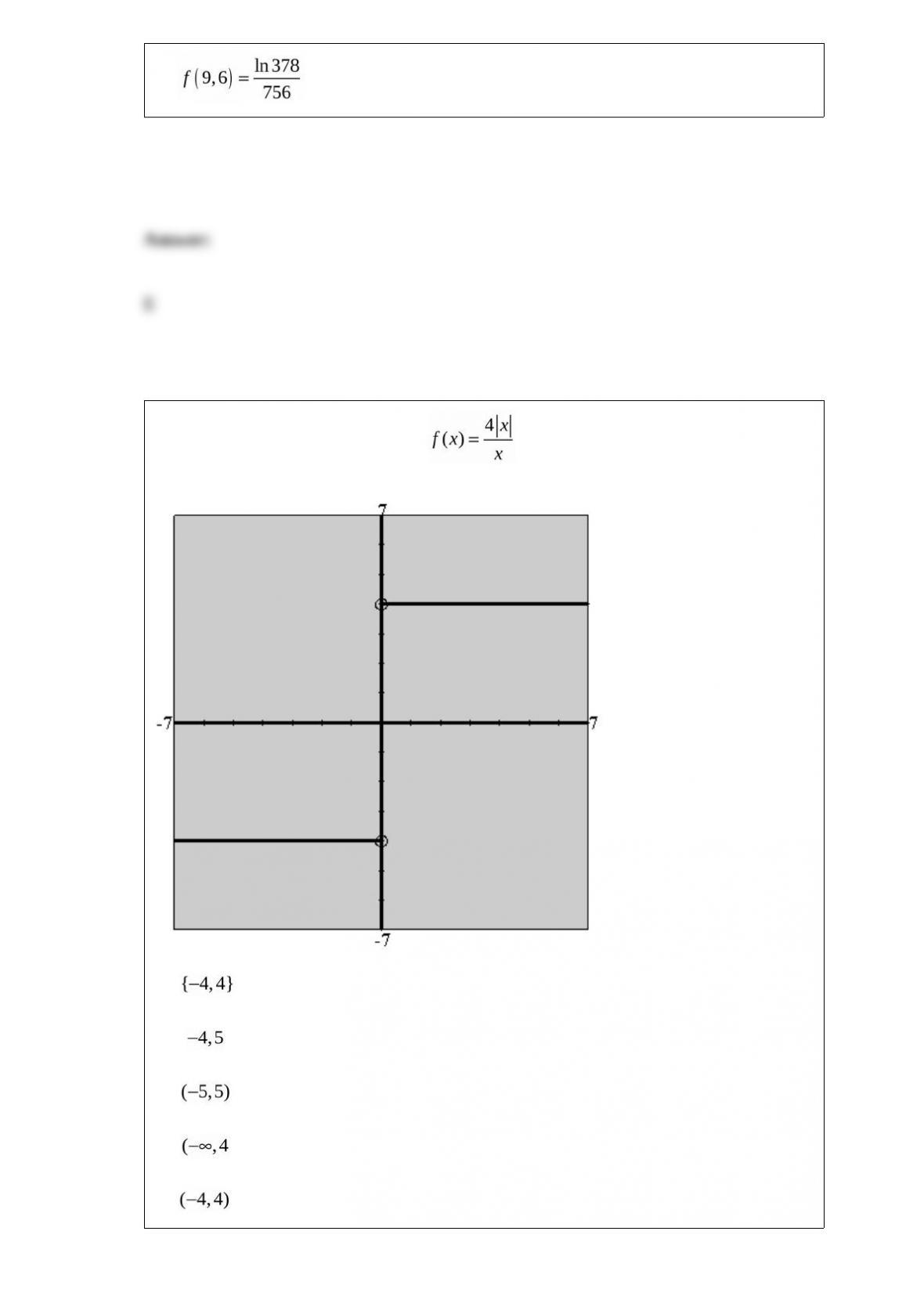
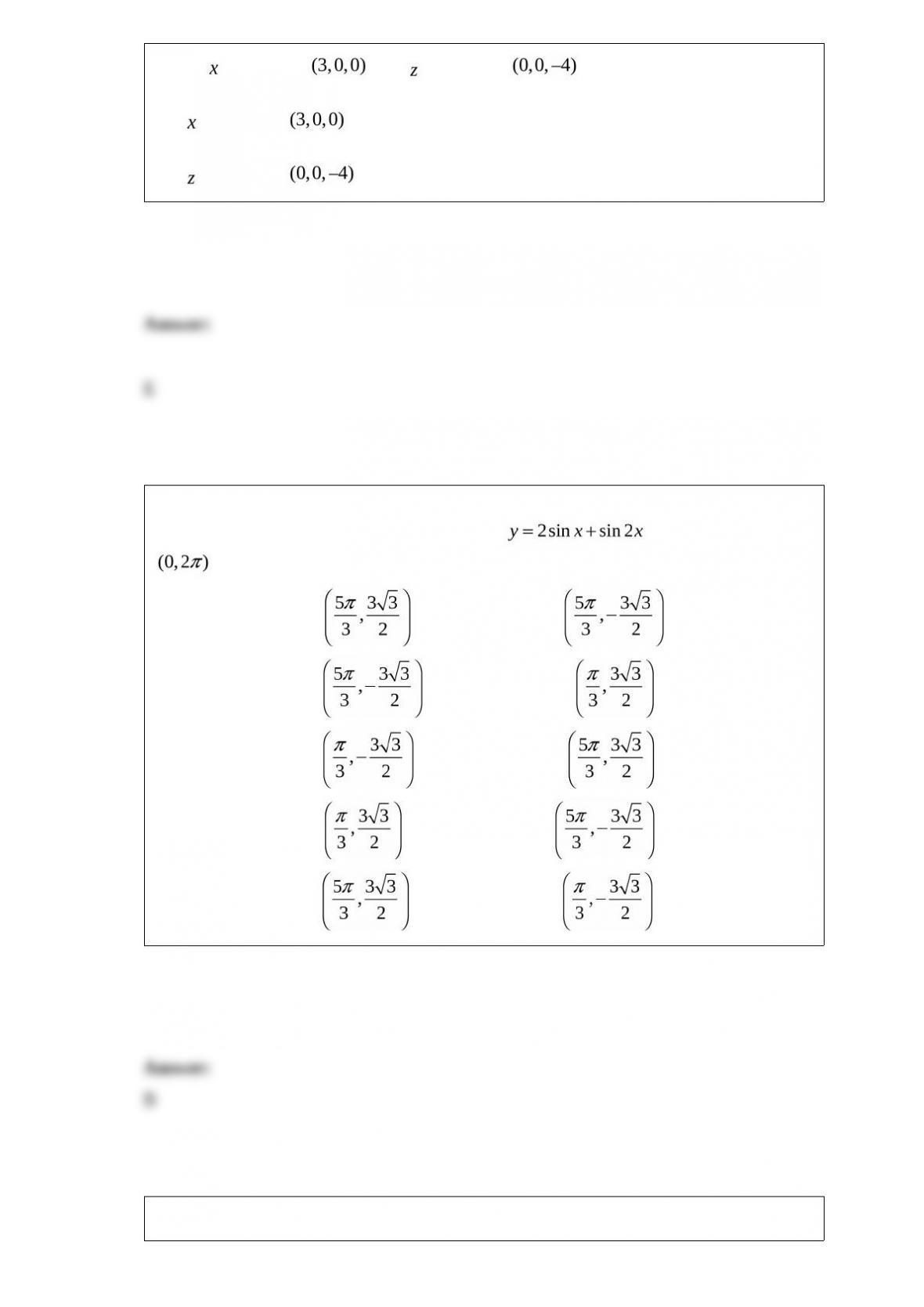
just come in, the probability that the next call will come within the next t minutes is
. Find the probability that the next call will come within the next
minute. Round your answer to two decimal places.
A) 4.08%
B) 0.41%
C) 195.92%
D) 6.31%
E) 3.95%
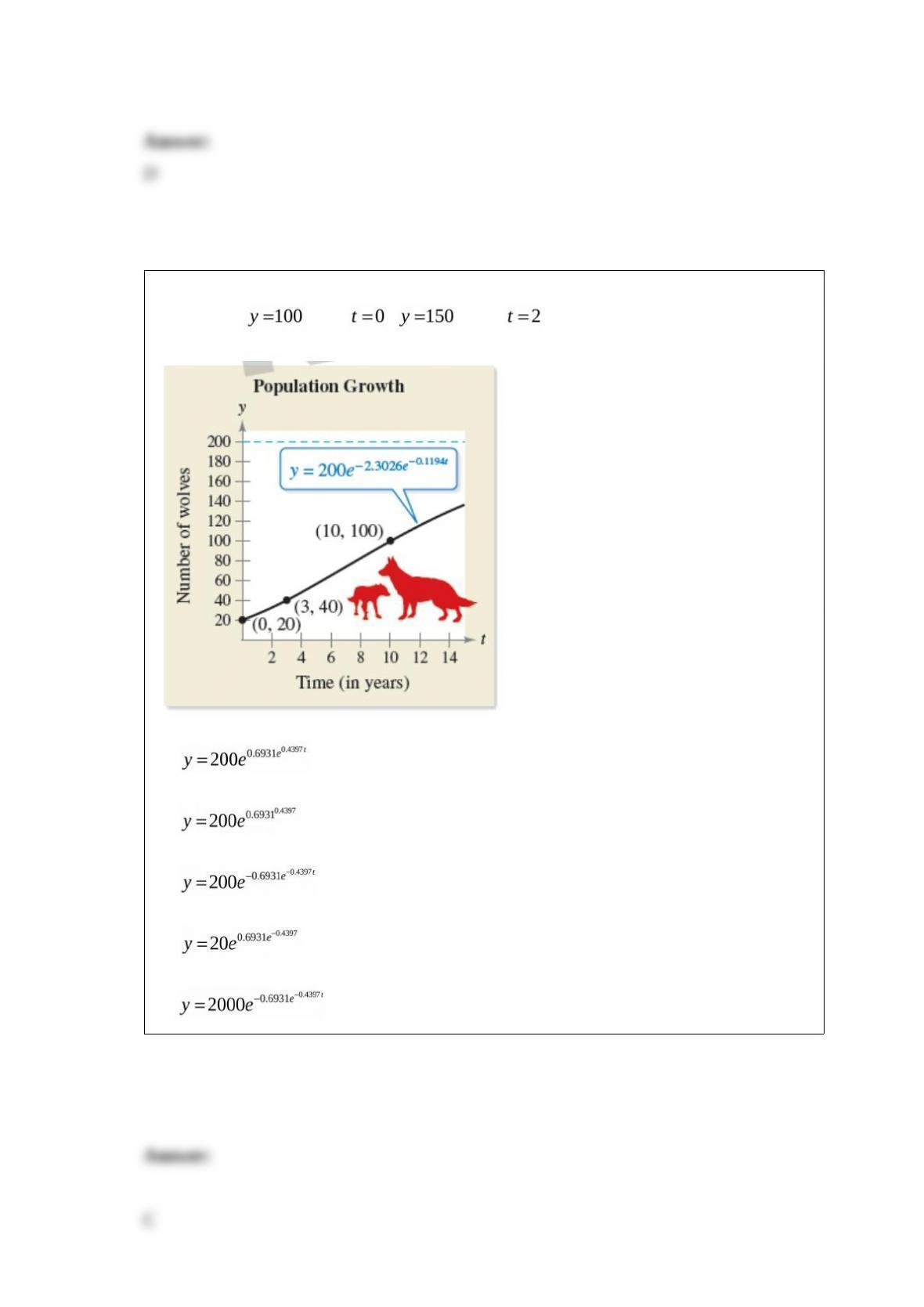
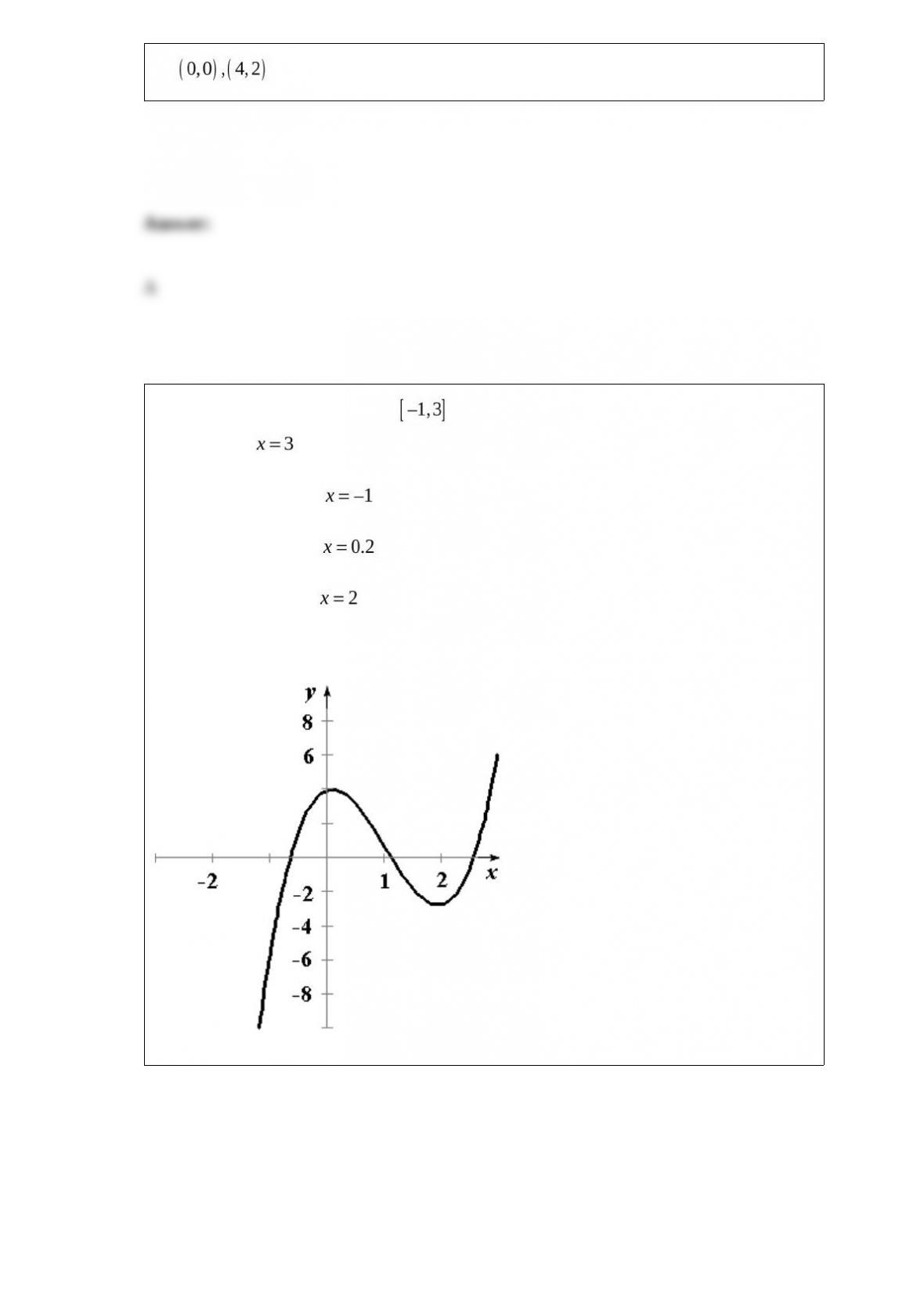
The number of people who donated to a certain organization between 1975 and 1992
can be modeled by the equation
donors, where t is the number of years after 1975. Find the inflection point(s) from
through , if any exist.
A) There are no inflection points from through .
B) There is one inflection point at .
C) There are inflection points at and .
D) There is one inflection point at .
E) There are inflection points at , , and .
A population of eight beavers has been introduced into a new wetlands area. Biologists
estimate that the maximum population the wetlands can sustain is 60 beavers. After 3
years, the population is 15 beavers. The population follows a Gompertz growth model.
How many beavers will there be in the wetlands after 10 years?
A) 34 beavers
B) 30 beavers
C) 33 beavers
D) 31 beavers
E) 39 beavers
Use the regression capabilities of a graphing utility or a spreadsheet to find the least
squares regression line for the points . Round
your answer to three decimal places.
A)
B)
C)
D)
E)
Find the sum of the convergent series.
A)
B)
C)
D)
E)
A compact disc can have an angular speed up to 3160 radians per minute. At this
angular speed, how many revolutions per minute would the CD make? Round your
answer to the nearest integer.
A) 123
B) 144
C) 923
D) 503
E) 72
Use the Gompertz growth model described to find the population y as a function of time
t (in years). when ; when
A)
B)
C)
D)
E)
Find the radian measure of the given angle.
150o
A)
B)
C)
D)
E)
Use implicit differentiation to find .
A)
B)
C)
D)
E)
Determine the point(s), (if any), at which the graph of the function has a horizontal
tangent.
A)
B) and
C) and
D)
E) There are no points at which the graph has a horizontal tangent.
Find the point(s), if any, at which the graph of f has a horizontal tangent line.
A)
B)
C)
D)
E)
Graph a function on the interval having the following characteristics. Absolute
maximum at
Absolute minimum at
Relative maximum at
Relative minimum at
A)
B)
C)
D)
E)
Find the indefinite integral of .
A)
B)
C)
D)
E)
The time t (in hours) required for a new employee to successfully learn to operate a
machine in a manufacturing process is described by the probability density function
over the interval . Find the probability that a new employee
will learn to operate the machine in more than 2 hours but less than 5 hours.
A) 0.4498
B) 0.1264
C) 0.3714
D) 0.0981
E) 0.2733
Sketch the graph of the following probability density function and locate the mean on
the graph.
A)
mean : 1.600
B)
mean : 2.012
C)
mean : 0.555
D)
mean : 1.848
E)
mean : 0.714
Find the y-value at the relative minima, and use a graphing utility to check your result.
A)
B)
C)
D)
E) does not exist
For , calculate to three decimal places.
A) 1.609
B) “40.236
C) “13.047
D) “1.000
E) “8.047