If
A)
B)
C)
D)
E)
Find the general solution satisfies the differential equation. Then find the particular
solution that satisfies the initial condition. General Solution: Differential
equation: Initial condition:
A)
B)
C)
D)
E)
Write the first five terms of the sequence.
an =
A)
B)
C)
D)
E)
Write the first-order linear differential equation in standard form.
A)
B)
C)
D)
E)
Find the indefinite integral.
A)
B)
C)
D)
E)
When the price of a glass of lemonade at a lemonade stand was $1.75, 400 glasses were
sold. When the price was lowered to $1.50, 500 glasses were sold. Assume that the
demand function is linear and that the marginal and fixed costs are $0.10 and $ 25,
respectively. Find the profit P as a function of x, the number of glasses of lemonade
sold.
A)
B)
C)
D)
E)
Use the Trapezoidal Rule to approximate the value of the definite integral
. Round your answer to three decimal places.
A) 6.7643
B) 2.7931
C) 2.7955
D) 4.6552
E) 4.6615
Find the derivative of the function.
A)
B)
C)
D)
E)
Write the equation of the line through that is parallel to
A)
B)
C)
D)
E)
A coin is tossed five times. Describe the event A that at least four tails occur.
A)
B)
C)
D)
E)
Find .
A)
B)
C)
D)
E)
A company manufactures two types of sneakers: running shoes and basketball shoes.
The total revenue from x1 units of running shoes and y1 units of basketball shoes is:
,
where x1 and x2 are in thousands of units. Find x1 and x2 so as to maximize the revenue.
A)
B)
C)
D)
E)
For the function given, find
A)
B)
C)
D)
E)
Which of the following is the correct graph of the given equation?
A)
B)
C)
D)
E)
Find the degree measure of the given angle.
A) 50.0o
B) 315.0o
C) 51.4o
D) 102.9o
E) 100.3o
Sketch the graph of the function and describe the interval(s) on which
the function is continuous.
A) and
B) and
C) and
D) and
E) none of these choices
Find the indefinite integral.
A)
B)
C)
D) integral does not exist
E) none of the above
A manufacturer has an order for 800 units of fine paper that can be produced at two
locations. Let and be the numbers of units produced at the two plants. Find the
number of units that should be produced at each plant to minimize the cost if the cost
function is given by .
A) units and units
B) units and units
C) units and units
D) units and units
E) units and units
Find the mean, variance, and standard deviation of the normal density function
over . Do not use integration.
A)
expected value mean : 4
variance: 36
standard deviation: 6
B)
expected value mean : 36
variance: 4
standard deviation: 6
C)
expected value mean : 36
variance: 6
standard deviation: 4
D)
expected value mean : 6
variance: 4
standard deviation: 36
E)
expected value mean : 4
variance: 6
standard deviation: 36
Solve the triangle for the indicated side.
A) side
B) side
C) side
D) side
E) side
The repeating decimal is expressed as a geometric series
. Write the decimal as the ratio of two integers.
A)
B)
C)
D)
E)
Use the properties of exponents to simplify the expression .
A)
B) 25
C)
D)
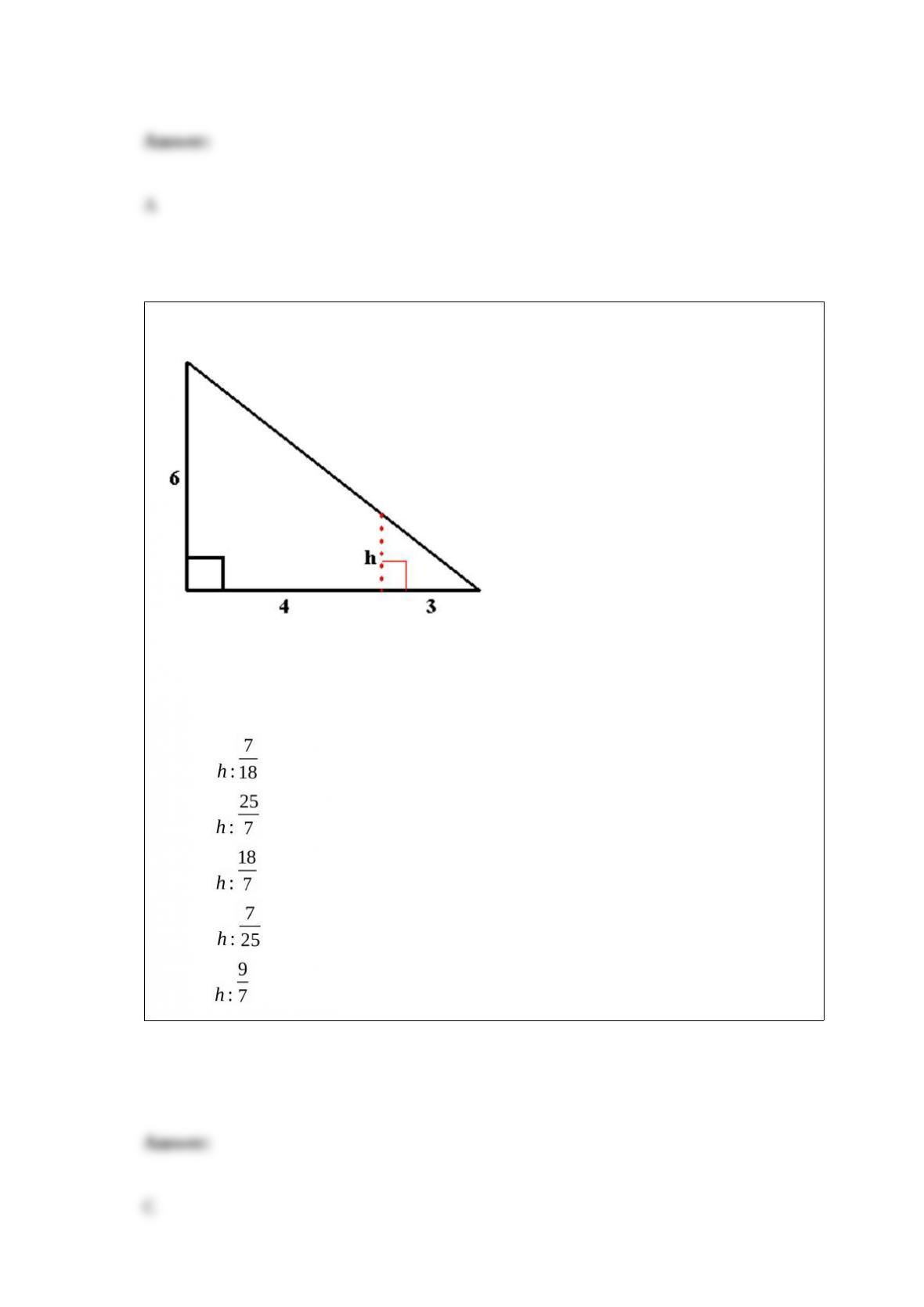
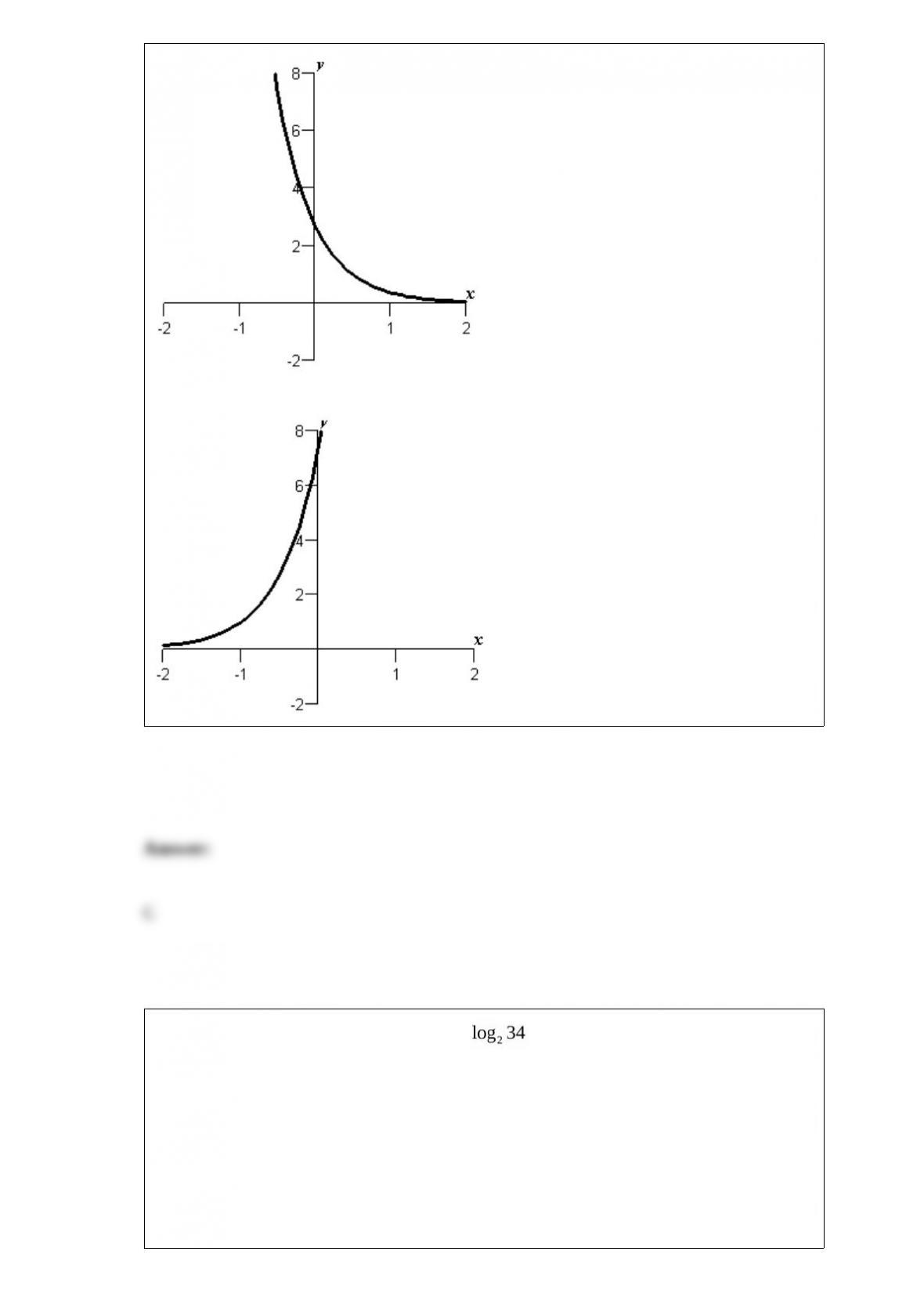
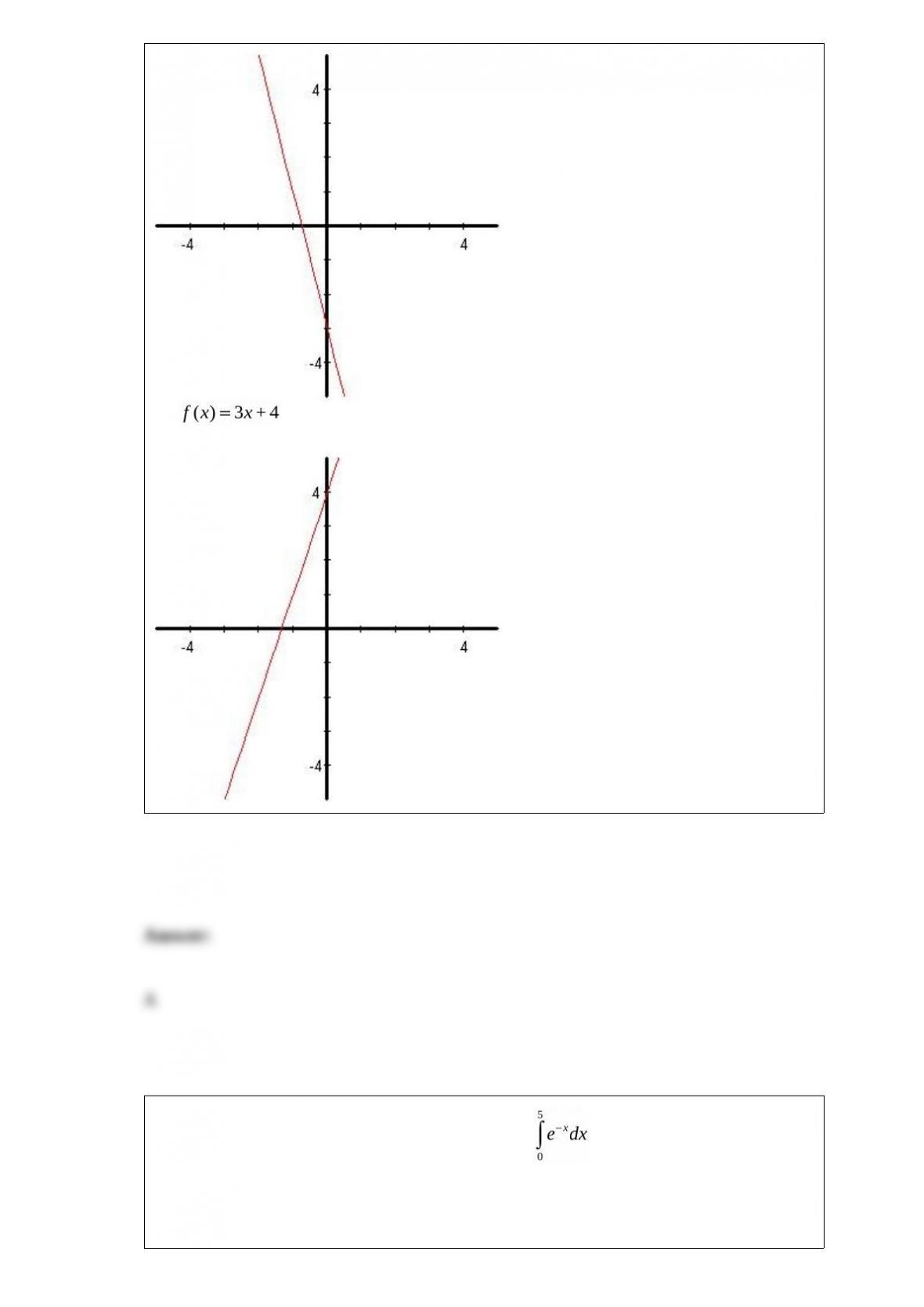
E) 625
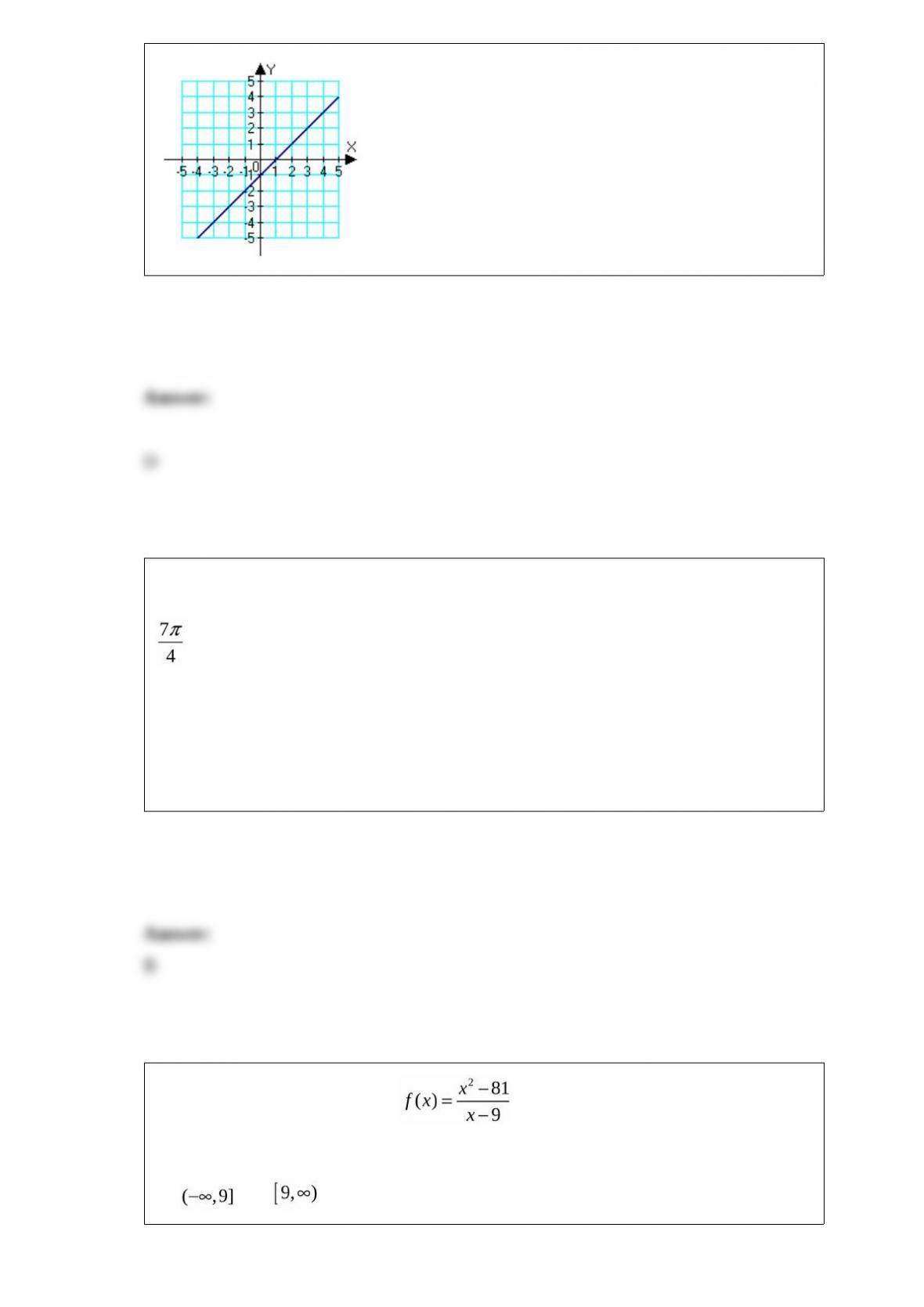
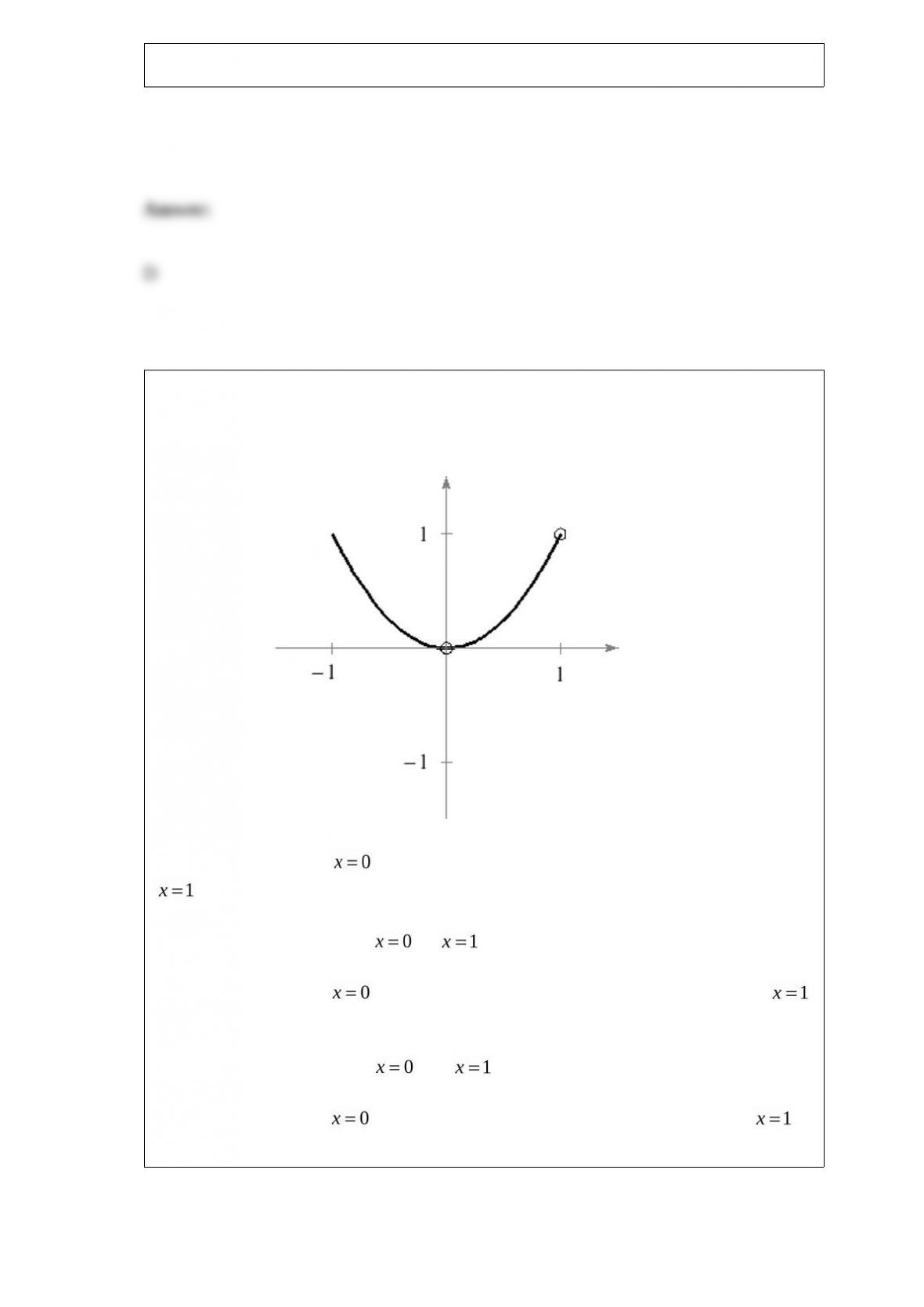
Approximate the critical numbers of the function shown in the graph and determine
whether the function has a relative maximum, a relative minimum, an absolute
maximum, an absolute minimum, or none of these at each critical number on the
interval shown.
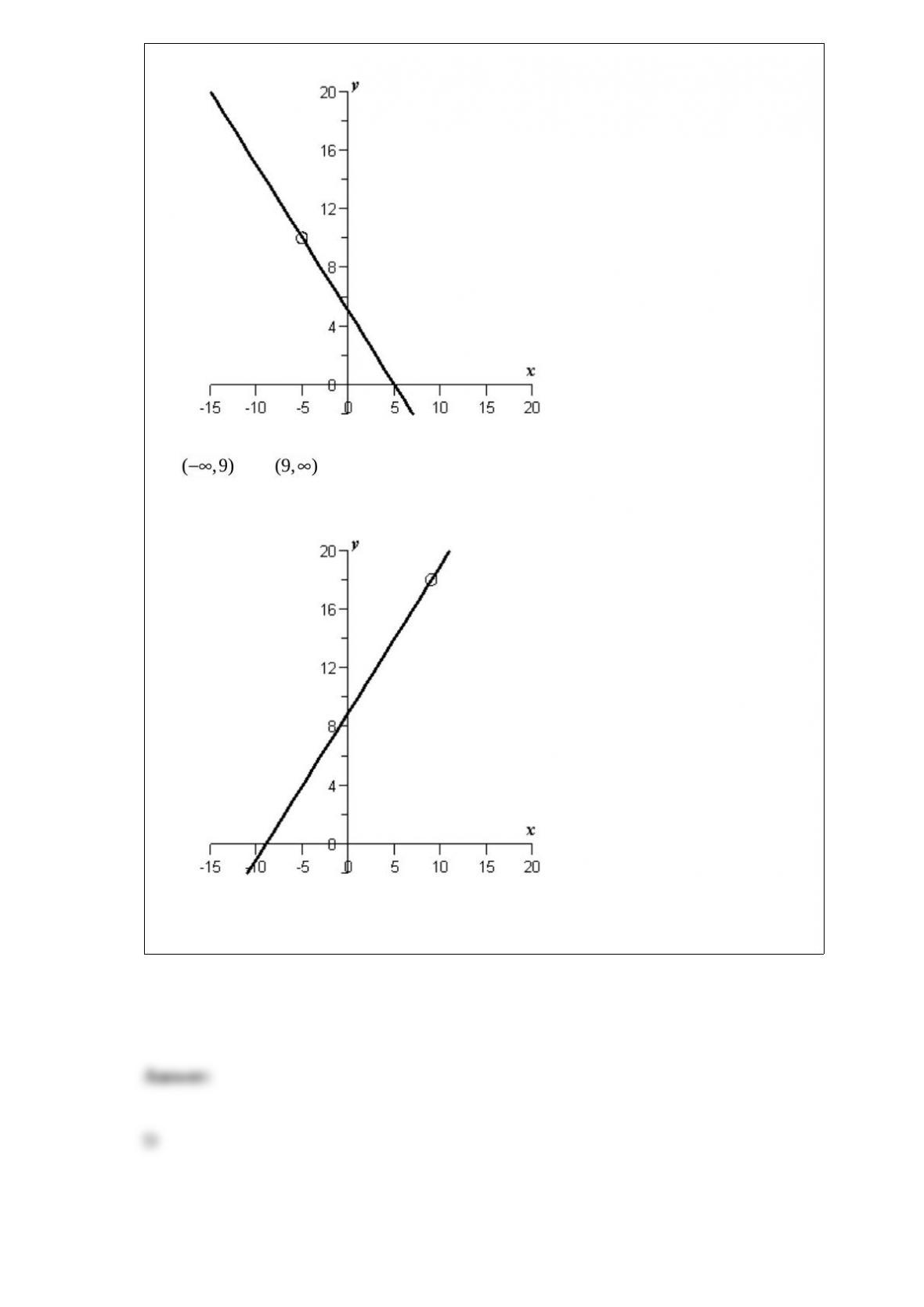
A) The critical number yields an absolute maximum and the critical number
yields an absolute minimum..
B) Both the critical numbers & yield an absolute maximum.
C) The critical number yields an absolute minimum and the critical number
yields an absolute maximum.
D) Both the critical numbers and yield an absolute minimum.
E) The critical number yields a relative minimum and the critical number
yields a relative maximum.
The value V of a machine years after it is purchased is inversely proportional to the
square root of . The initial value of the machine is 10,000. Find the rate of
depreciation when . Round your answer to two decimal places.
A) “603.68 per year
B) “1889.82 per year
C) 1767.77 per year
D) 447.21 per year
E) “1207.36 per year
Sketch the graph of the function .
A)
B)
C)
D)
E)
Use a calculator to evaluate the logarithm . Round your answer to three decimal
places.
A) 0.197
B) 2.444
C) 6.360
D) 3.717
E) 5.087
The isotope has a half-life of 5,715 years. Given an initial amount of 11 grams of
the isotope, how many grams will remain after 1,000 years? After 10,000 years? Round
your answers to four decimal places.
A) 6.8205 gm, 2.2896 gm
B) 3.8974 gm, 1.3083 gm
C) 9.7436 gm, 3.2708 gm
D) 11.6923 gm, 3.9250 gm
E) 5.8462 gm, 1.9625 gm
Identify a function that has the given characteristics and then sketch the function.
A)
B)
C)
D)
E)
Decide whether the integral is proper or improper.
A) The integral is improper.
B) The integral is proper.
A rectangular box is resting on the -plane with one vertex at the origin. The opposite
lies in the plane Find the dimensions that maximize the volume. (Hint: Maximize
subject to the constraint ).
A) 15 units 12 units 5 units
B) 11 units 9 units 5 units
C) 10 units 9 units 6 units
D) 15 units 10 units 6 units
E) 12 units 11 units 7 units
Use the Vertical Line Test to determine which of the following graphs shows y as a
function of x.
A)
B)
C)
D)
E)
Determine whether the statement is true or false. If it is false, explain why or give an
example that shows it is false.
If
A) True
B) False. The product rule is