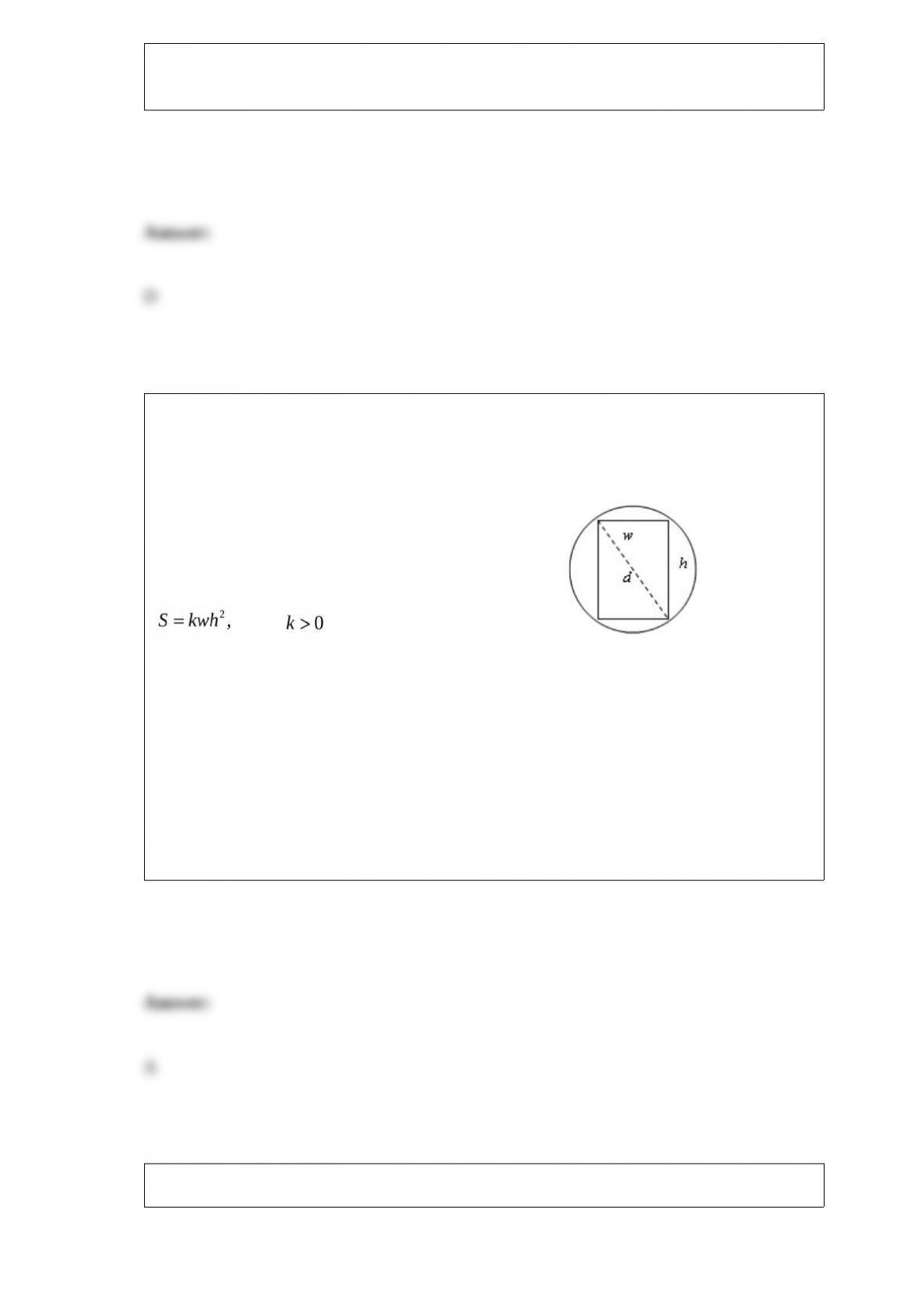
Minimum cost. From a tract of land, a developer plans to fence a rectangular region and
then divide it into two identical rectangular lots by putting a fence down the middle.
Suppose that the fence for the outside boundary costs per foot and the fence for the
middle costs per foot. If each lot contains square feet, find the dimensions of
each lot that yield the minimum cost for the fence.
A) Dimensions are 48.07 ft for the side parallel to the divider and 85.29 ft for the other
side.
B) Dimensions are 85.29 ft for the side parallel to the divider and 48.07 ft for the other
side.
C) Dimensions are 64.03 ft for the side parallel to the divider and 64.03 ft for the other
side.
D) Dimensions are 60.37 ft for the side parallel to the divider and 67.91 ft for the other
side.
E) Dimensions are 67.91 ft for the side parallel to the divider and 60.37 ft for the other
side.
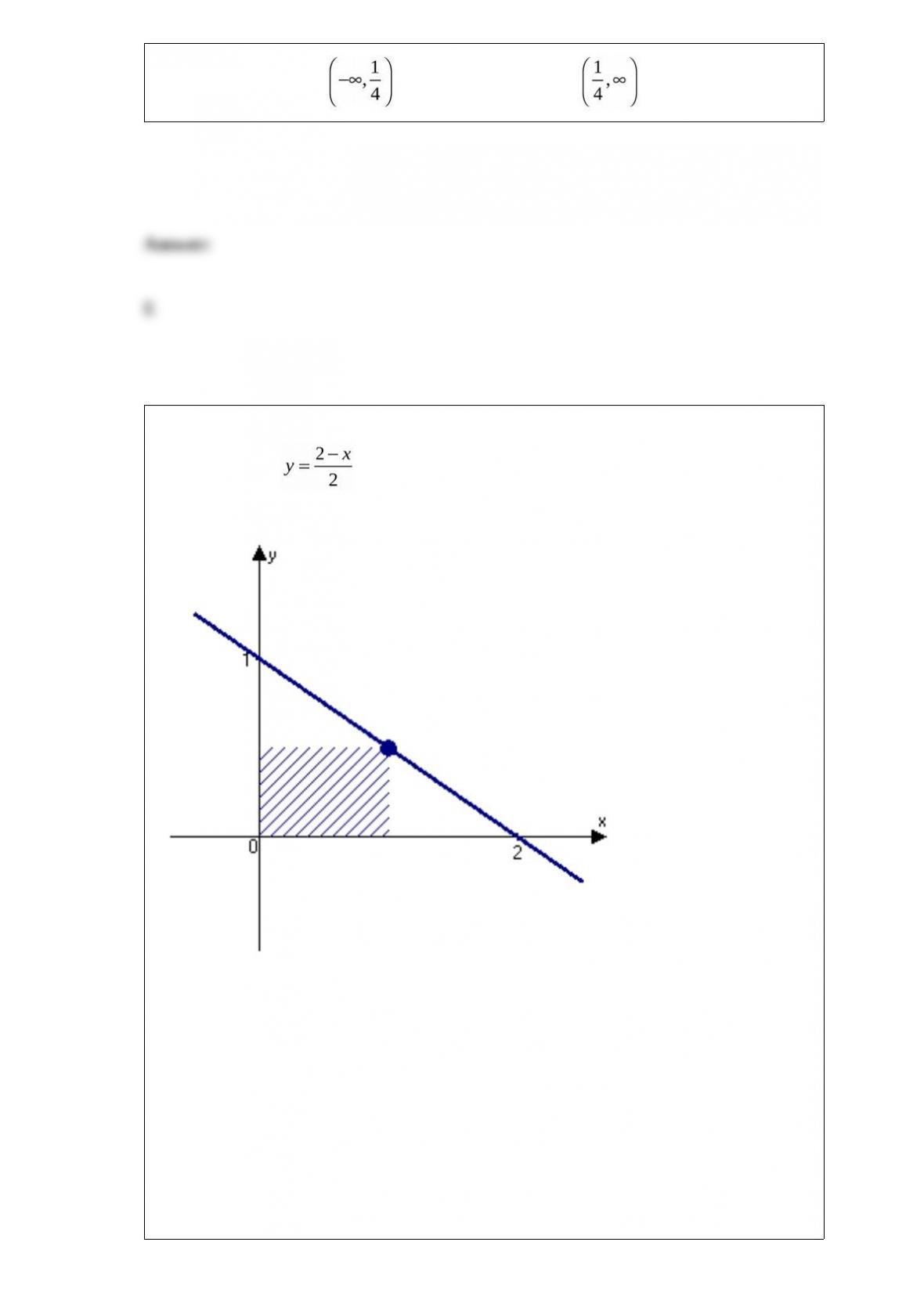
Determine the open intervals on which the graph of is concave
downward or concave upward.
A) concave downward on
B) concave downward on ; concave upward on
C) concave upward on ; concave downward on
D) concave downward on ; concave upward on
E) concave upward on ; concave downward on
Find the dimensions of the rectangle of maximum area bounded by the x-axis and y-axis
and the graph of .
A) length 0.75; width 0.625
B) length 1; width 0.5
C) length 0.25; width 0.875
D) length 0.5; width 0.75
E) none of the above
Use Lagrange multipliers to find the given extremum. In each case, assume that
and are positive.
Maximize Constraints
A)
B)
C)
D)
E)
The graph shows the number of visitors V to a national park in hundreds of thousands
during a one-year period, where t = 1 represents January. Estimate the rate of change of
V over the interval . Round your answer to the nearest hundred thousand visitors
per year.
A) 176.92 hundred thousand visitors per year
B) 328.57 hundred thousand visitors per year
C) 166.67 hundred thousand visitors per year
D) 383.33 hundred thousand visitors per year
E) 766.67 hundred thousand visitors per year
Find given the probability distribution.
A) 0.440
B) 1.000
C) 0.790
D) 0.650
E) 0.250
A wooden beam has a rectangular cross section of height h and width w (see figure).
The strength S of the beam is directly proportional to the width and the square of the
height. What are the dimensions of the strongest beam that can be cut from a round log
of diameter d = 23 inches? Round your answers to two decimal places. [Hint:
where is the proportionality constant.]
A) w = 13.28 inches and h = 18.78 inches
B) w = 7.67 inches and h = 21.68 inches
C) w = 19.92 inches and h = 11.50 inches
D) w = 16.26 inches and h = 16.27 inches
E) w = 18.78 inches and h = 13.28 inches
Use separation of variables to find the general solution of the differential equation.
A)
B)
C)
D)
E)
Find the derivative of the function.
A)
B)
C)
D)
E)
Complete the table and use the result to estimate the limit.
x
f(x)
A) 0.142857
B) 0.642857
C) 0.517857
D) 0.767857
E) “0.232143
If find and
A)
B)
C)
D)
E)
Find of , .
A)
B)
C)
D)
E) none of these choices
Medication. The number of milligrams x of a medication in the bloodstream t hours
after a dose is taken can be modeled by . Find the maximum value of
x. Round your answer to two decimal places.
A) 2.65 mg
B) 755.93 mg
C) 1663.04 mg
D) 8.20 mg
E) 1500.40 mg
An employee of a delivery company earns 22.50 per hour driving a delivery van in an
area where gasoline costs 2.50 per gallon. When the van is driven at a constant speed
s (in miles per hour, with ), the van gets miles per gallon. Determine
the most economical speed s for a 100-mile trip on an interstate highway.
A) The most economical speed is 47.0 mph.
B) The most economical speed is 43.0 mph.
C) The most economical speed is 22.5 mph.
D) The most economical speed is 45.0 mph.
E) The most economical speed is 48.0 mph.
Volume. A rectangular box with a square base is to be formed from a square piece of
metal with 36-inch sides. If a square piece with side x is cut from each corner of the
metal and the sides are folded up to form an open box, the volume of the box is
What value of x will maximize the volume of the box?
A) 18
B) 1
C) 6
D) 15
E) 9
Which of the following is the correct graph of ?
A)
B)
C)
D)
E)
Find the third derivative of the function .
A)
B)
C)
D)
E)
Write the following expression as a logarithm of a single quantity.
A)
B)
C)
D)
E) none of the above
Find the particular solution of the differential equation that satisfies the
initial condition y = 8 when x = 3, where is the general solution.
A)
B)
C)
D)
E)
Find the general solution of the first-order linear differential equation.
A)
B)
C)
D)
E)
Use a table of integrals to find the indefinite integral .
A)
B)
C)
D)
E)
For the function , use a graphing utility to complete the table and
estimate the limit as x approaches infinity.
x 100 101 102 103 104 105 106
f(x)
A) 0.6
B) 1.666667
C) 2.666667
D) 1.6
E) “0.4
Use integration by parts to evaluate .
A)
B)
C)
D)
E)
For the probability density function on the interval , find the
probability that . Round your answer to the nearest thousandth.
A) 0.088
B) 0.245
C) 0.224
D) 0.250
E) 0.264
An airplane flying at an altitude of 5 miles passes directly over a radar antenna. When
the airplane is 25 miles away (s = 25), the radar detects that the distance s is changing at
a rate of 250 miles per hour. What is the speed of the airplane? Round your answer to
the nearest integer.
A) 255 mi/hr
B) 236 mi/hr
C) 510 mi/hr
D) 128 mi/hr
E) 118 mi/hr
Solve the differential equation to find velocity v as a function of time t if when
The differential equation models the motion of two people on a toboggan after
consideration of the forces of gravity, friction, and air resistance.
A)
B)
C)
D)
E)
Find an equation of the graph that passes through the point and has the specified slope.
Then graph the equation. Point: , Slope:
A)
B)
C)
D)
E) None of the Above
Assume that the median sales prices of existing one family homes sold (in thousands of
dollars) in the United States from 1990 through 2005 are as given in the following
figure. Use the following figure to estimate the percent increase in the value of existing
one-family homes from 1997 to 1998.
A) 0.021%
B) 0.058%
C) 2.06%
D) 55.5%
E) 5.8%
Use the function to find
A)
B)
C)
D)
E)
Find the value for the function .
A) 734,208
B) 430,080
C) 221,185
D) 430,081
E) 3,403,776
Determine whether is a solution of the differential equation .
A)
B)
C)
D)
E)
Production. Suppose that the total number of units produced by a worker in t hours of
an 8-hour shift can be modeled by the production function
. Find the number of hours before the rate of production
is maximized. That is, find the point of diminishing returns.
A)
B)
C)
D)
E)