The rate of depreciation of a building is given by dollars per year,
Use the definite integral to find the total depreciation over the first years.
A)
B)
C)
D)
E)
Use a table of integrals with forms involving to find the integral.
A)
B)
C)
D)
E)
Use formal substitution to find the indefinite integral .
A)
B)
C)
D)
E)
A 21-foot ladder leaning against the side of a house makes a 78 angle with the ground
(see figure). How far up the side of the house does the ladder reach? Round your
answer to four decimal places.
A) 20.5411 feet
B) 21.4692 feet
C) 4.3661 feet
D) 4.4637 feet
E) 101.0044 feet
Find the derivative of the following function using the limiting
process.
A)
B)
C)
D)
E) either B or D
Sketch the graph of the function .
A)
B)
C)
D)
E)
Find all relative extrema of the function . Use the Second-Derivative Test
when applicable.
A) The relative maximum is .
B) The relative minimum is .
C) The relative maximum is .
D) The relative minimum is .
E) The relative maximum is .
Use a symbolic differentiation utility to find the Taylor polynomials (centred at zero) of
degrees (a) 2, (b) 4, (c) 6, (d) 8.
A)
B)
C)
D)
E)
Evaluate the integral
A)
B)
C)
D)
E)
The demand function for a product is modeled by . What is
the limit of the price as x increases without bound? Round your answer to two decimal
places where applicable.
A) The limit of the price as x increases without bound is -1.
B) The limit of the price as x increases without bound is 1.
C) The limit of the price as x increases without bound is 0.
D) The limit of the price as x increases without bound is .
E) The limit of the price as x increases without bound is .
Find the four second partial derivatives. Observe that the second mixed partials are
equal.
A)
B)
C)
D)
E)
Determine the area of the given region.
A)
B)
C)
D)
E) None of the above
Find .
A)
B)
C)
D)
E)
Find the derivative of the following function using the limiting process.
A)
B)
C)
D)
E) none of the above
Find the slope of the tangent line to the graph of the function below at the given
point.
A)
B)
C)
D)
E) none of the above
Find the radius of convergence centered at for the following function.
A) 3
B) 2
C) 0
D) 1
E)
Let be a random variable that is normally distributed with the given mean and
standard deviation . Find the probability using a symbolic
integration utility.
A) 0.5889
B) 0.6687
C) 0.7970
D) 0.6302
E) 0.5292
Sketch a graph of a function f having the following characteristics.
A)
B)
C)
D)
E)
Which of the following is a solution of the differential equation ?
A)
B)
C)
D)
E)
Examine the function given below for relative extrema and saddle points.
A) The function has a relative maximum at .
B) The function has a relative minimum at .
C) The function has a saddle point at .
D) The function has a relative maximum at .
E) The function has a relative minimum at .
The utility function is a measure of utility (or satisfaction) derived by a
person from the consumption of two products x and y. Suppose the utility function is
. Determine the marginal utility of product x.
A)
B)
C)
D)
E)
Analytically determine the location(s) of any horizontal asymptote(s).
A)
B)
C) ,
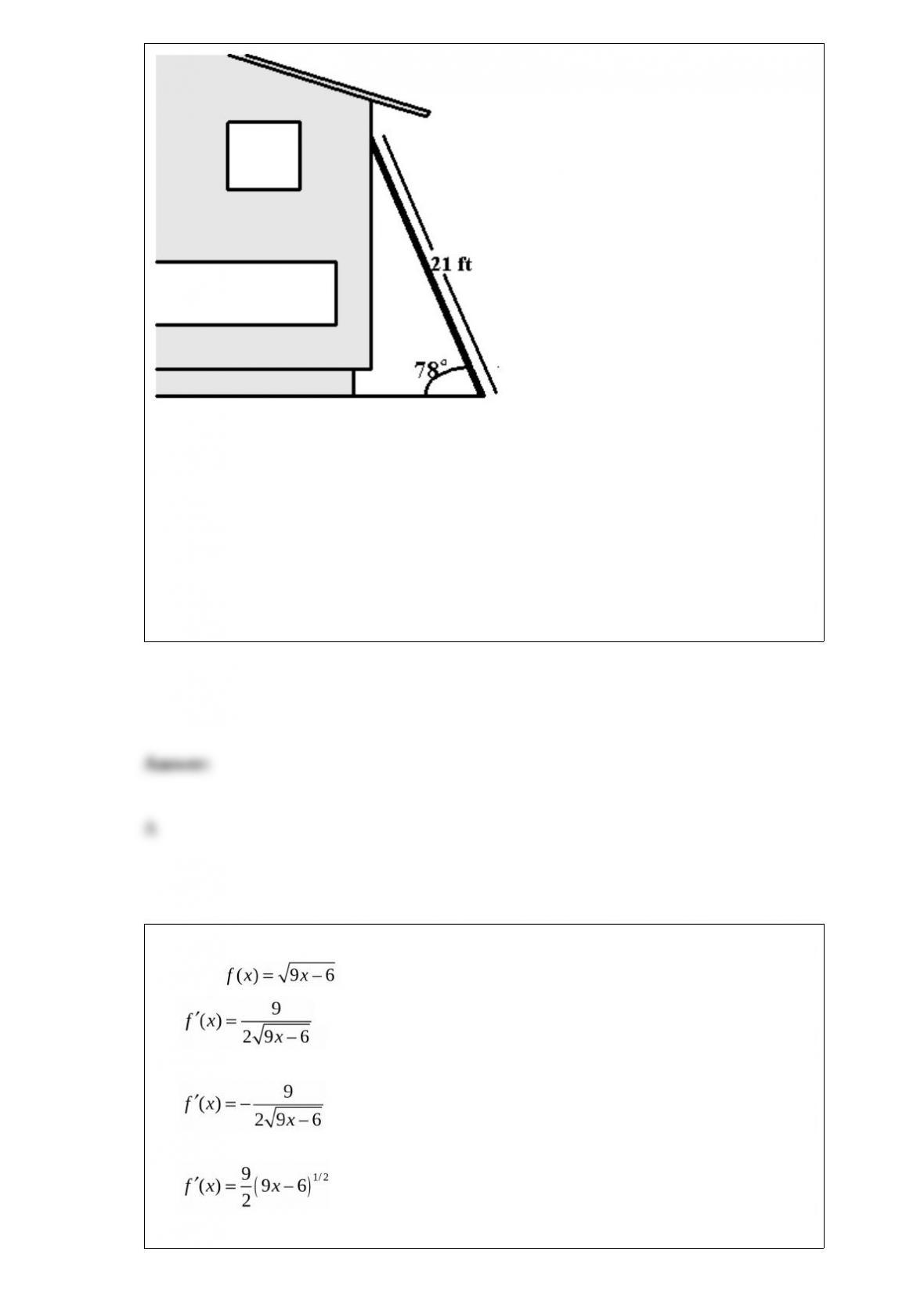
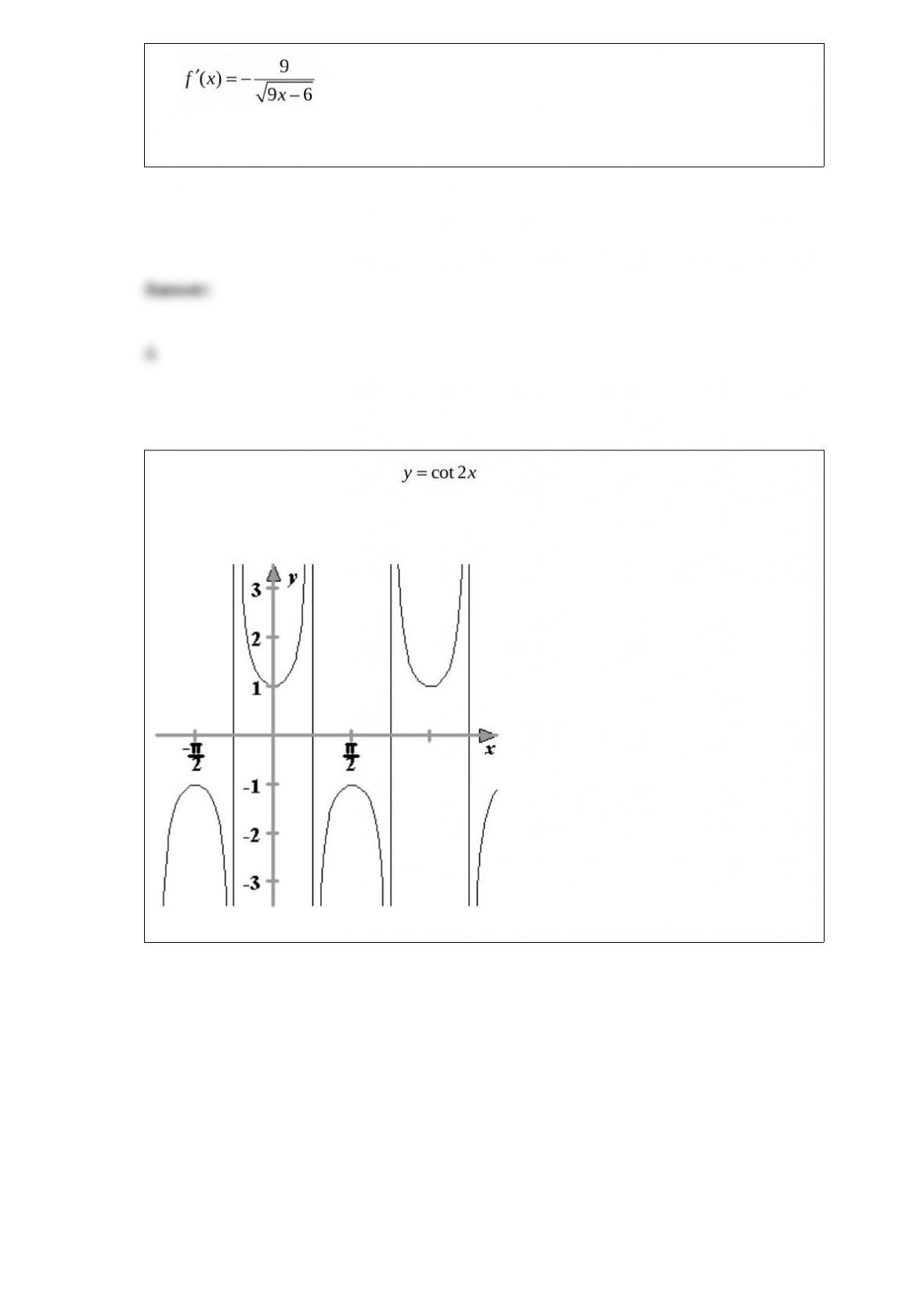
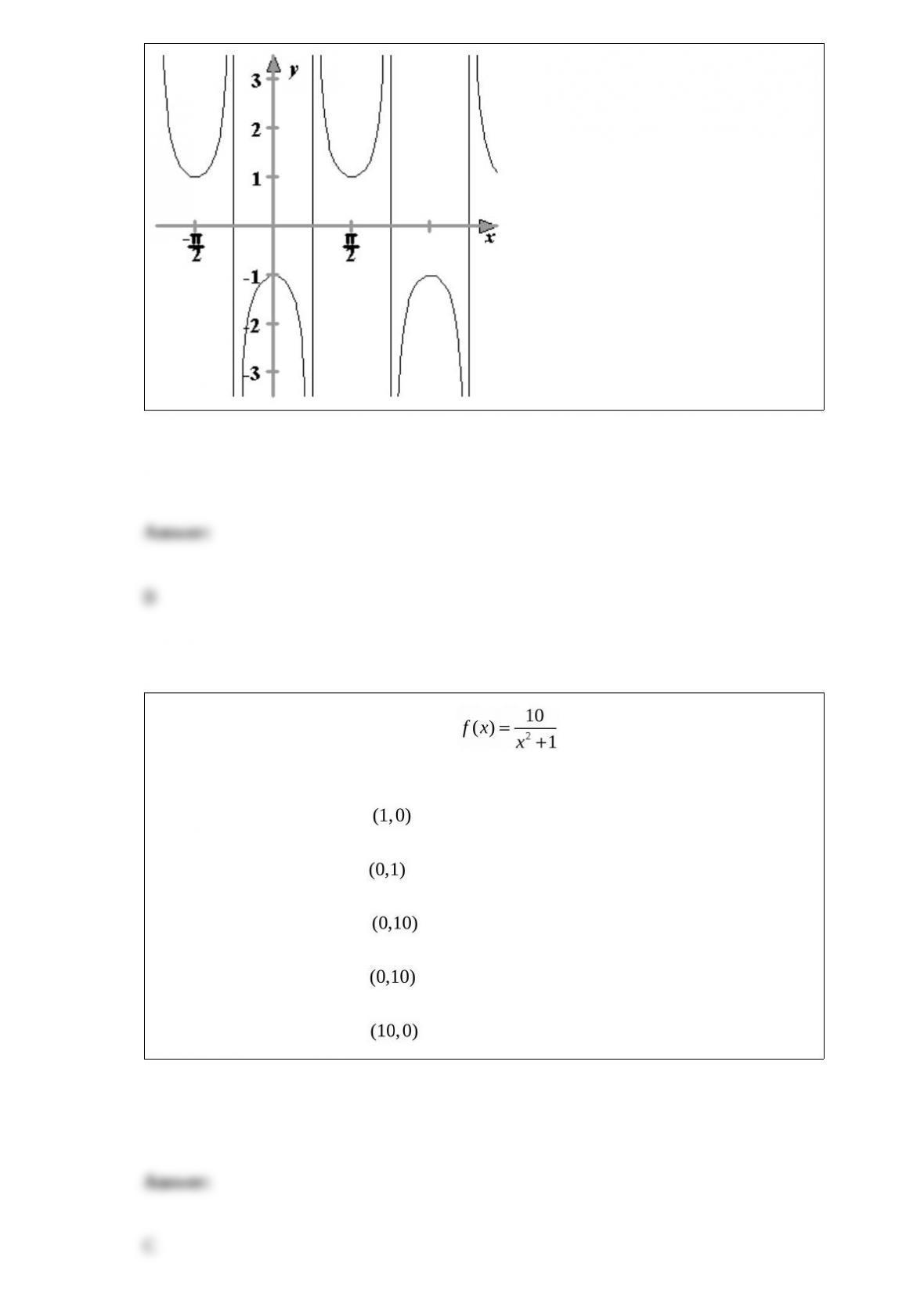
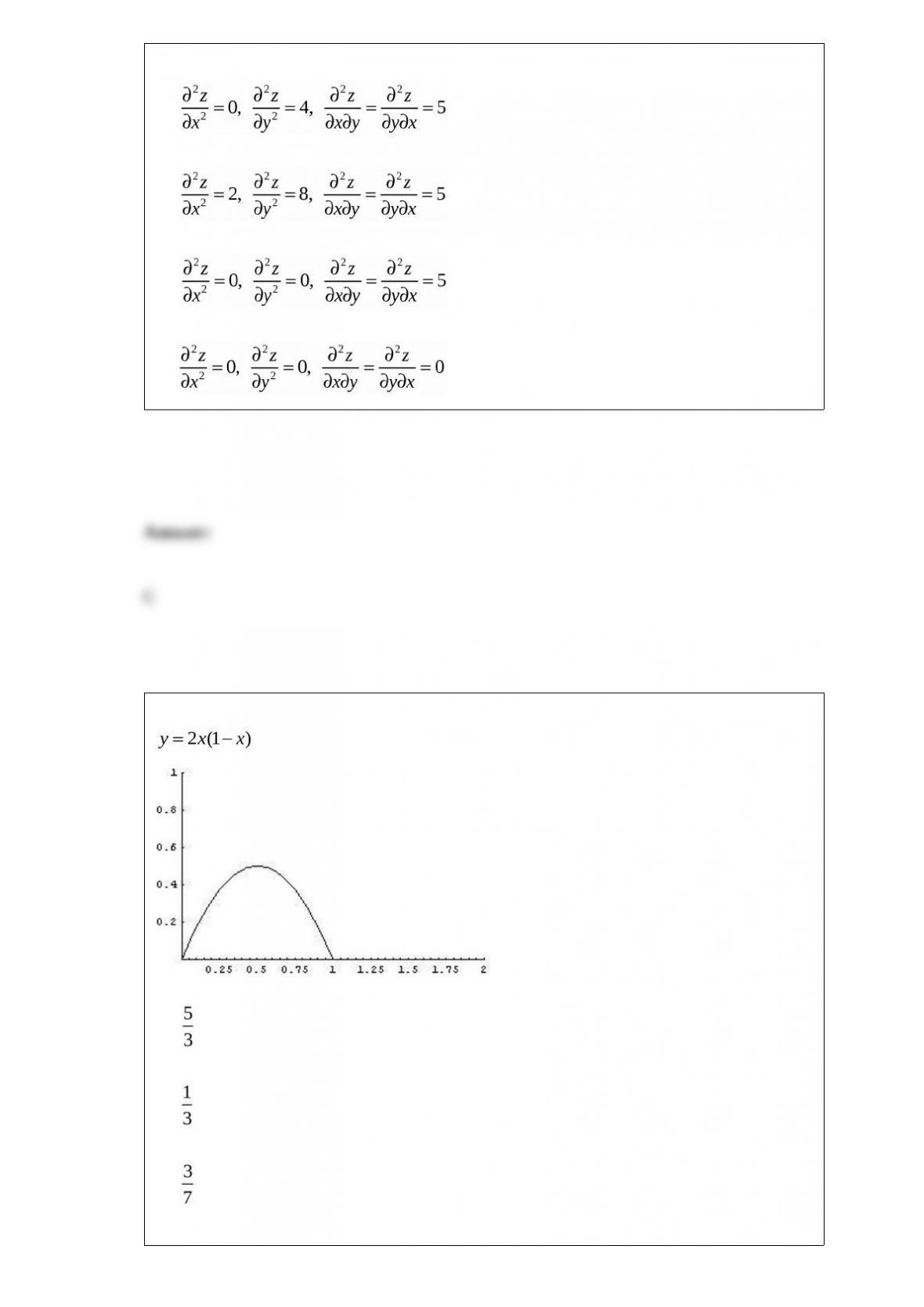
D)
E) no horizontal asymptotes
The cost of producing x units of a product is modeled by
. Find the minimum average cost analytically. Round your answer to two decimal
places.
A) 200.00 dollars per unit
B) 199.40 dollars per unit
C) 199.18 dollars per unit
D) 201.41 dollars per unit
E) 199.28 dollars per unit
A factory is polluting a river such that at every mile down river from the factory an
environmental expert finds 15% less pollutant than at the preceding mile. If the
pollutant’s concentration is 500 ppm (parts per million) at the factory, what is its
concentration 15 miles down river?
A) 75.00 ppm
B) 225.00 ppm
C) 43.68 ppm
D) 588.24 ppm
E) 51.38 ppm
Sketch the graph of the function
A)
B)
C)
D)
E)
Find the power series for the function using the power series for .
A)
B)
C)
D)
E)
Use the initial condition to find the particular solution of the differential equation.
, when
A)
B)
C)
D)
E)
The variable cost for the production of a calculator is 16.25 and the initial investment
is 530,000. Use differentials to approximate the change in the cost C for a one-unit
increase in production when , where x is the number of units produced.
A) 1300000.00 dollars
B) 17.25 dollars
C) 1301000.00 dollars
D) 16.25 dollars
E) 26.25 dollars
Find the average value of over the region R: square with vertices
.
A)
B)
C)
D)
E)
Use separation of variables to find the general solution of the differential equation.
A)
B)
C)
D)
E)
Find the second derivative of the function.
A)
B)
C)
D)
E) None of the above
Use integration by parts to evaluate . Note that evaluation may require
integration by parts more than once.
A)
B)
C)
D)
E)
Find the derivative of the function . State which differentiation
rule(s) you used to find the derivative.
A) 1, Product Rule.
B) 1, Quotient Rule
C) 5, Product Rule.
D) 5, Quotient Rule
E) x+3, Product Rule.
Consider a certificate of deposit that pays 14% (annual percentage rate) on an initial
deposit of $4000. The balance after 14 years is . Estimate ,
where is the length of the compounding period (in years). Round your answer to the
nearest hundredth.
A) 28,397.31
B) 1471.52
C) 4000.00
D) 56,000.00
E) 4560.00
Use the initial condition to find the particular solution of the differential equation.
, when
A)
B)
C)
D)
E)