A 100-gallon tank is full of a solution containing 25 pounds of a concentrate. Starting at
time distilled water is admitted to the tank at the rate of 5 gallons per minute, and
the well-stirred solution is withdrawn at the same rate. (a) Find the amount of the
concentrate in the solution as a function of by solving the differential equation
(b) Find the time required for the amount of concentrate in the tank to
reach 15 pounds.
A) a. b.
B) a. b.
C) a. b.
D) a. b.
E) a. b.
The graph of f is shown in the figure. Sketch a graph of the derivative of f.
A)
B)
C)
D)
E)
Find such that the distance between the points and is 10.
A) 13 or “13
B) “3 or 3
C) 13 or “3
D) “11 or 11
E) 15 or “15
Evaluate the definite integral . Round your answer to three decimal places.
A) 20.210
B) 16.873
C) 32.580
D) 26.395
E) 4.504
Simplify the expression using the given function definition.
A) “8
B) “12
C) “13
D) “16
E) undefined
Determine two coterminal angles (one positive and one negative) for each angle. Give
the answers in radians.
A) positive: negative:
B) positive: negative:
C) positive: negative:
D) positive: negative:
E) positive: negative:
Evaluate the improper integral if it converges, or state that it diverges.
A)
B)
C)
D)
E) diverges
The red figure is translated to a new position in the plane to form the blue figure. Find
the vertices of the transformed figure from the following graph. (In case your exam is
printed in black and white – the red figure has one vertex at (0,0)).
A)
B)
C)
D)
E)
Differentiate the given function.
A)
B)
C)
D)
E)
Identify the open intervals where the function is increasing or
decreasing.
A) decreasing: ; increasing:
B) increasing: ; decreasing:
C) increasing on
D) decreasing on
E) none of the above
A Taylor polynomial approximation of is given below. Use a graphing
utility to graph both functions.
A)
B)
C)
D)
E)
Find .
A) 4
B) 0
C)
D) “4
E) inf
Buses arrive and depart from a college every 40 minutes. The probability density
function for the waiting time t (in minutes) for a person arriving at the bus stop is
on the interval . Find the probability that the person will wait no
longer than 20 minutes.
A)
B)
C)
D)
E)
Find the open intervals on which the function is increasing or decreasing.
A) The function is increasing on the interval , and decreasing on the intervals
and .
B) The function is increasing on the interval , and decreasing on the
intervals and .
C) The function is increasing on the interval , and decreasing on the intervals
and .
D) The function is decreasing on the interval , and increasing on the intervals
and .
E) The function is decreasing on the interval , and increasing on the
intervals and .
Use the given information to write an equation for y.
A)
B)
C)
D)
E)
Determine the range of the function .
A) [
B)
C)
D)
E)
Find the cosine of .
A)
B)
C)
D)
E)
A function and its graph are given. Use the graph to find the vertical asymptotes, if they
exist, where Confirm your results analytically.
A)
B)
C)
D)
E) no vertical asymptotes
A company sells two products whose demand functions are given by and
. So, the total revenue is given by . Estimate the
average revenue if the price varies between $45 and $70 and the price varies
between 45 and 70.
A) $ 52,725
B) $ 54,875
C) $ 52,223
D) $ 53,740
E) $ 55,285
The cumulative sales (in thousands of units) of a new product after it has been on the
market for t years may be modeled by . During the first year, 5000 units
were sold. What is the saturation point for this product? How many units will be sold
after 6 years?
A) The saturation point for the market is 3000 units and 19,953 units will be sold after 6
years.
B) The saturation point for the market is 30,000 units and 27,366 units will be sold after
6 years.
C) The saturation point for the market is 30,000 units and 19,953 units will be sold after
6 years.
D) The saturation point for the market is 30,000 units and 20,076 units will be sold after
6 years.
E) The saturation point for the market is 3000 units and 27,366 units will be sold after 6
years.
Write the equation of the line passing through the given pair of points.
and
A)
B)
C)
D)
E)
Use the fourth-degree Taylor polynomial centered at for the function to
approximate . Round your answer to nearest thousandth.
A) 0.610
B) 0.607
C) 0.732
D) 0.718
E) 0.619
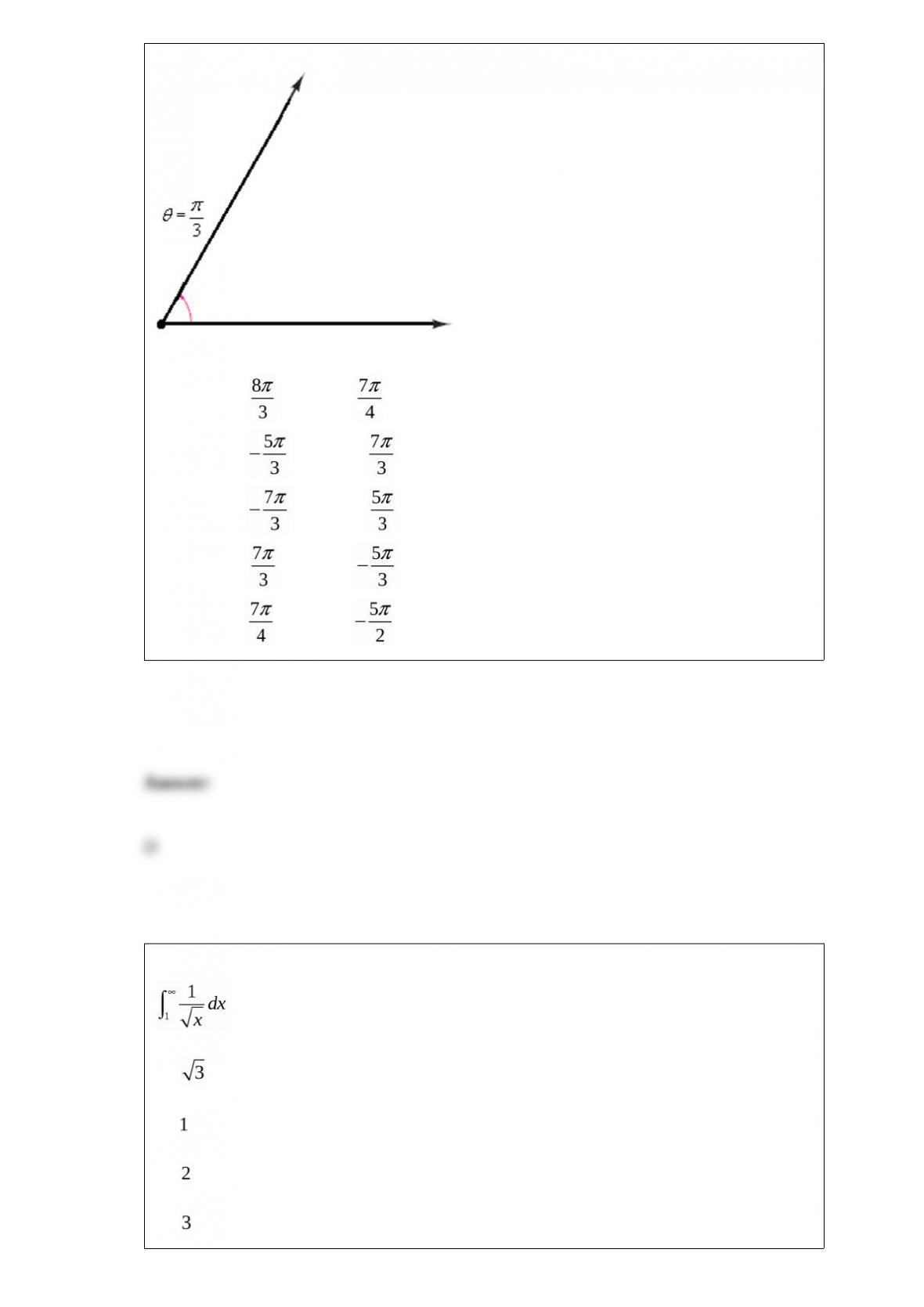
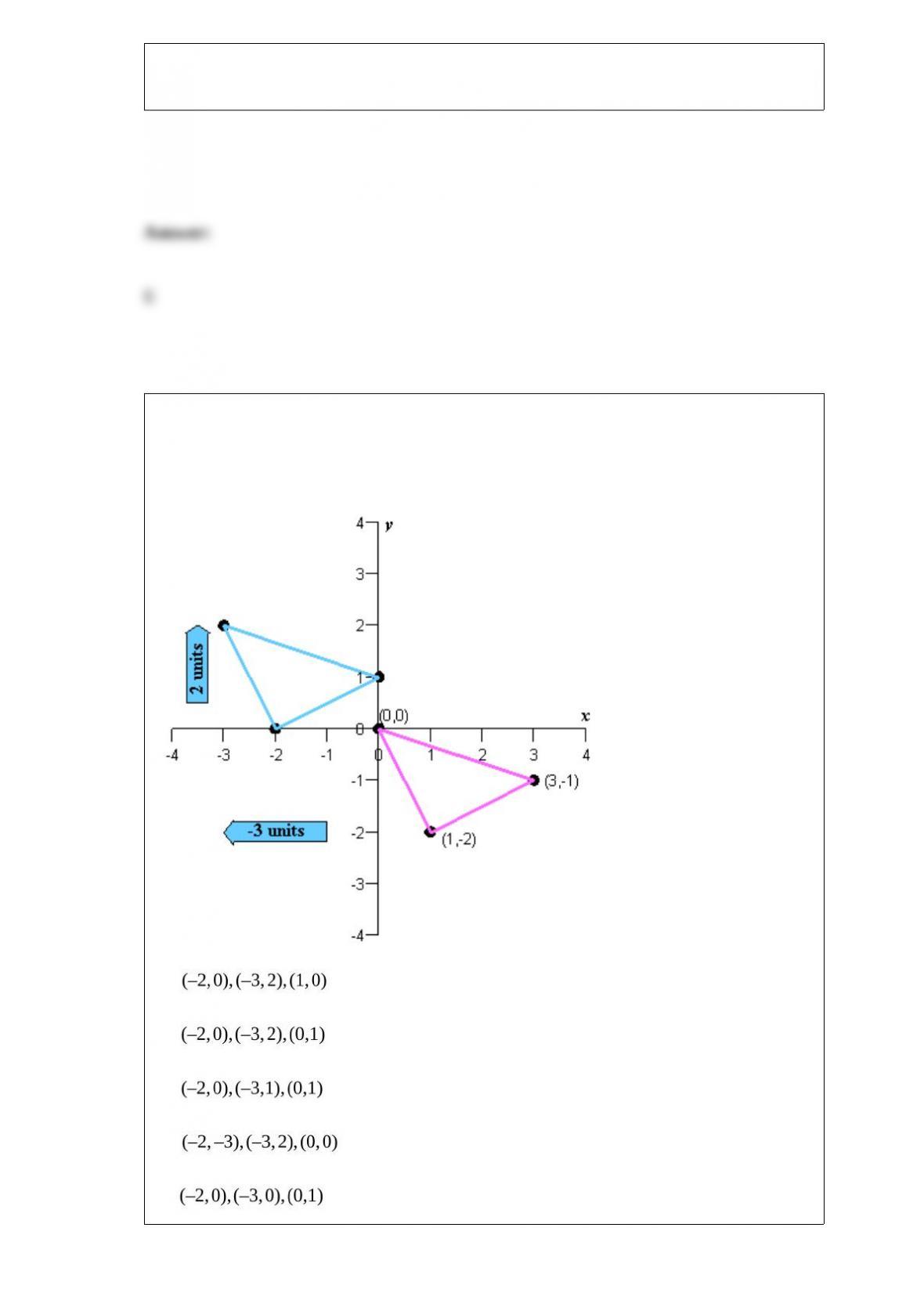
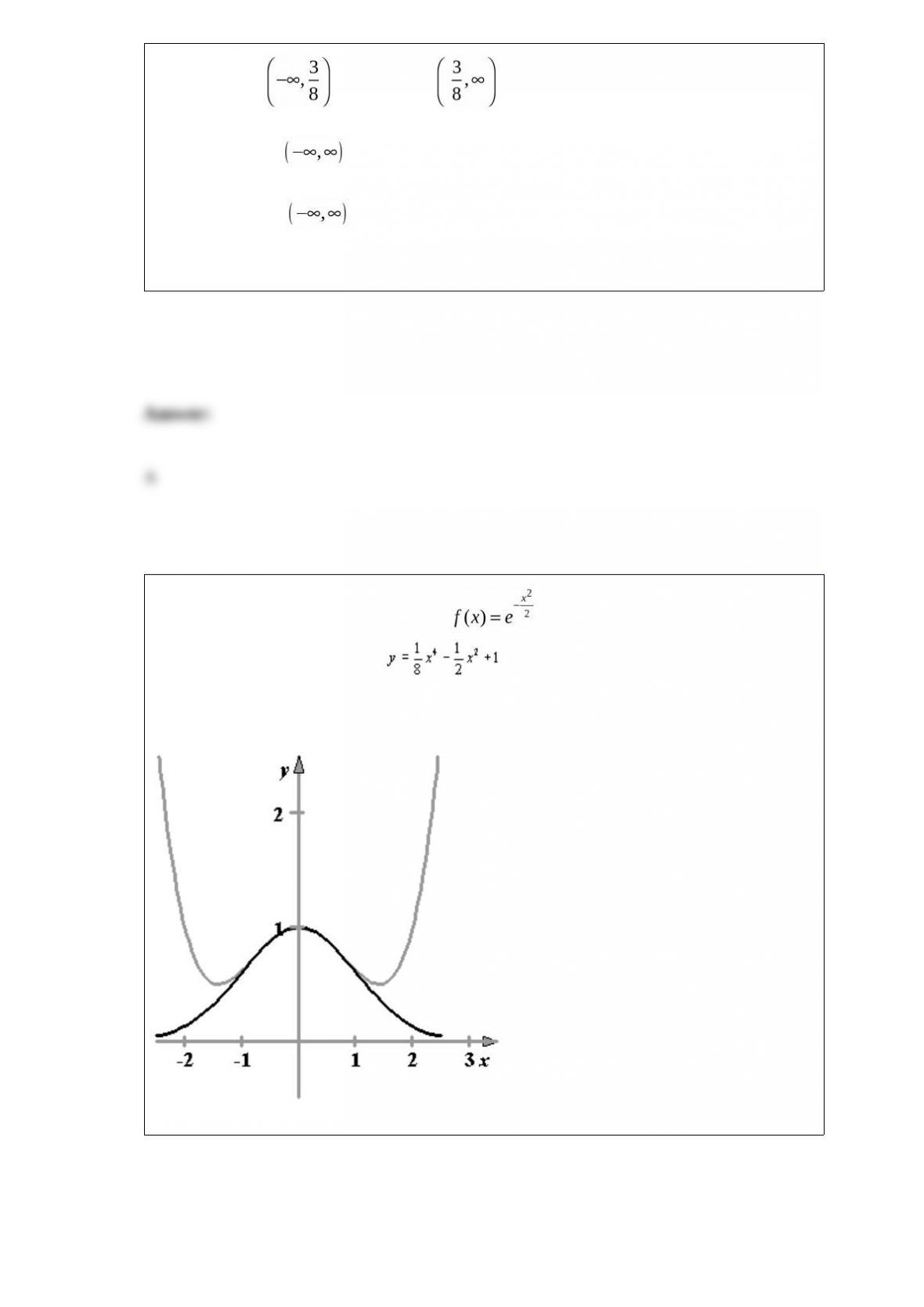
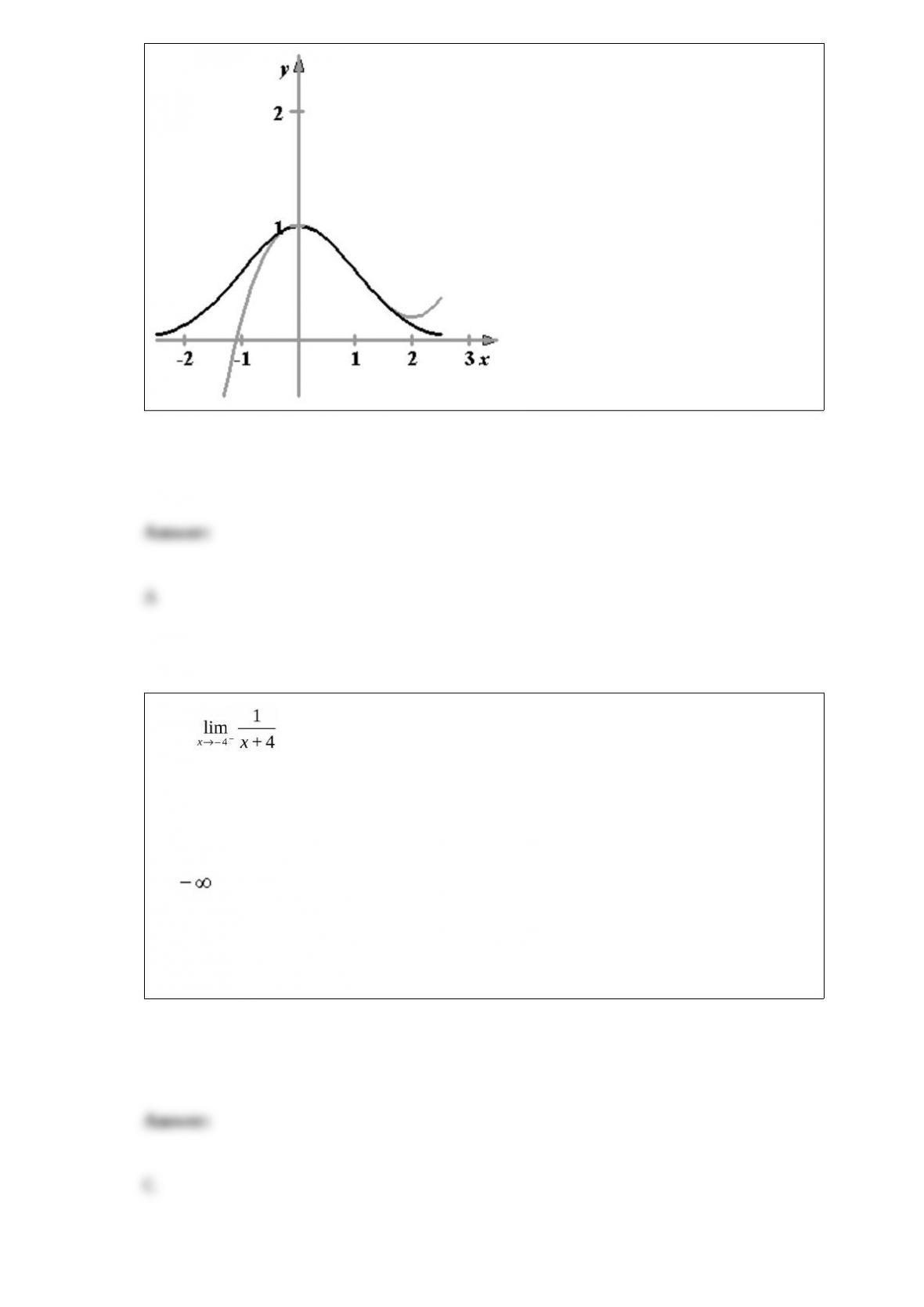
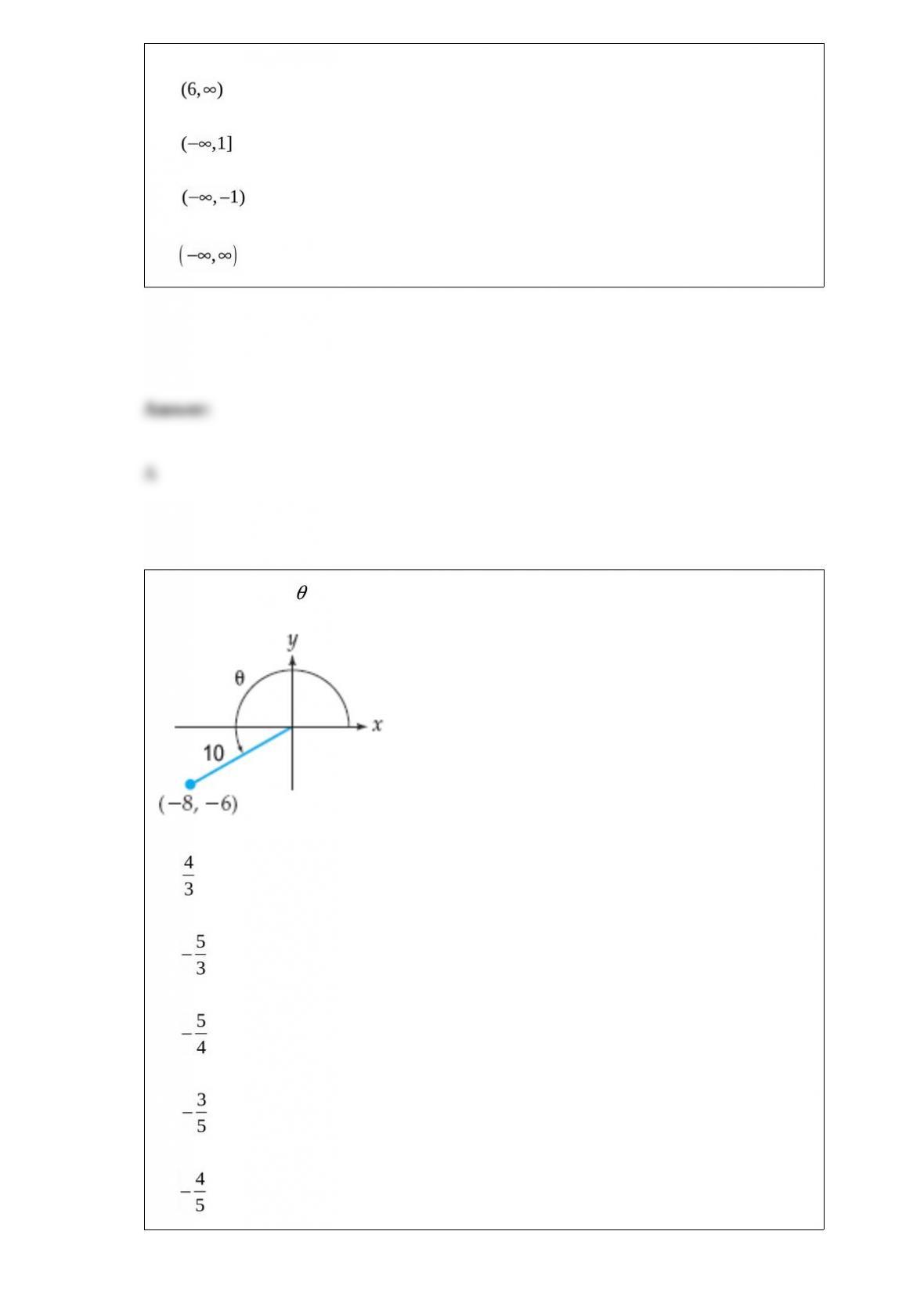
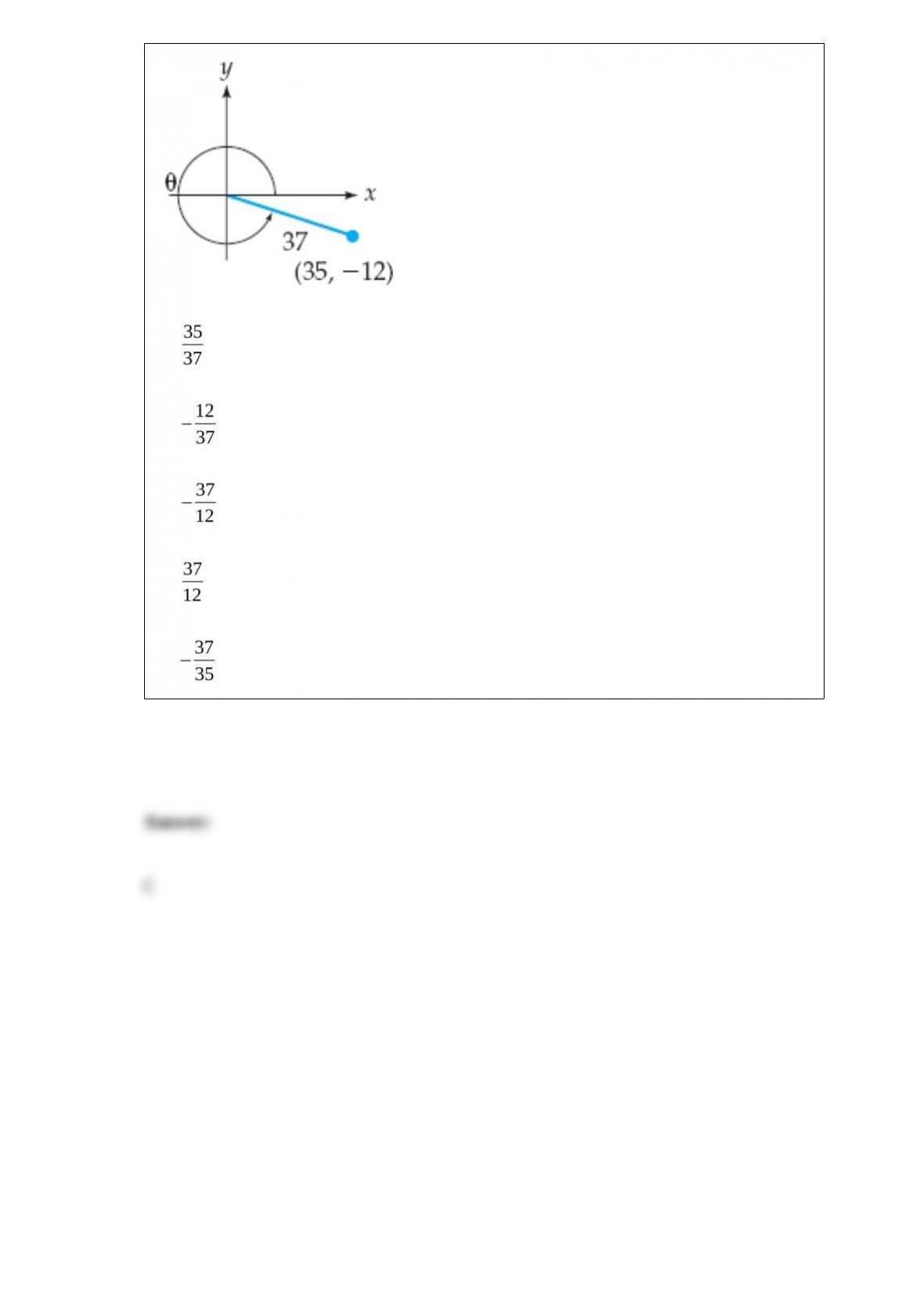
Find the slope m and y-intercept b of the line whose equation is given below.
A)
B)
C)
D)
E) Both m and b are undefined.
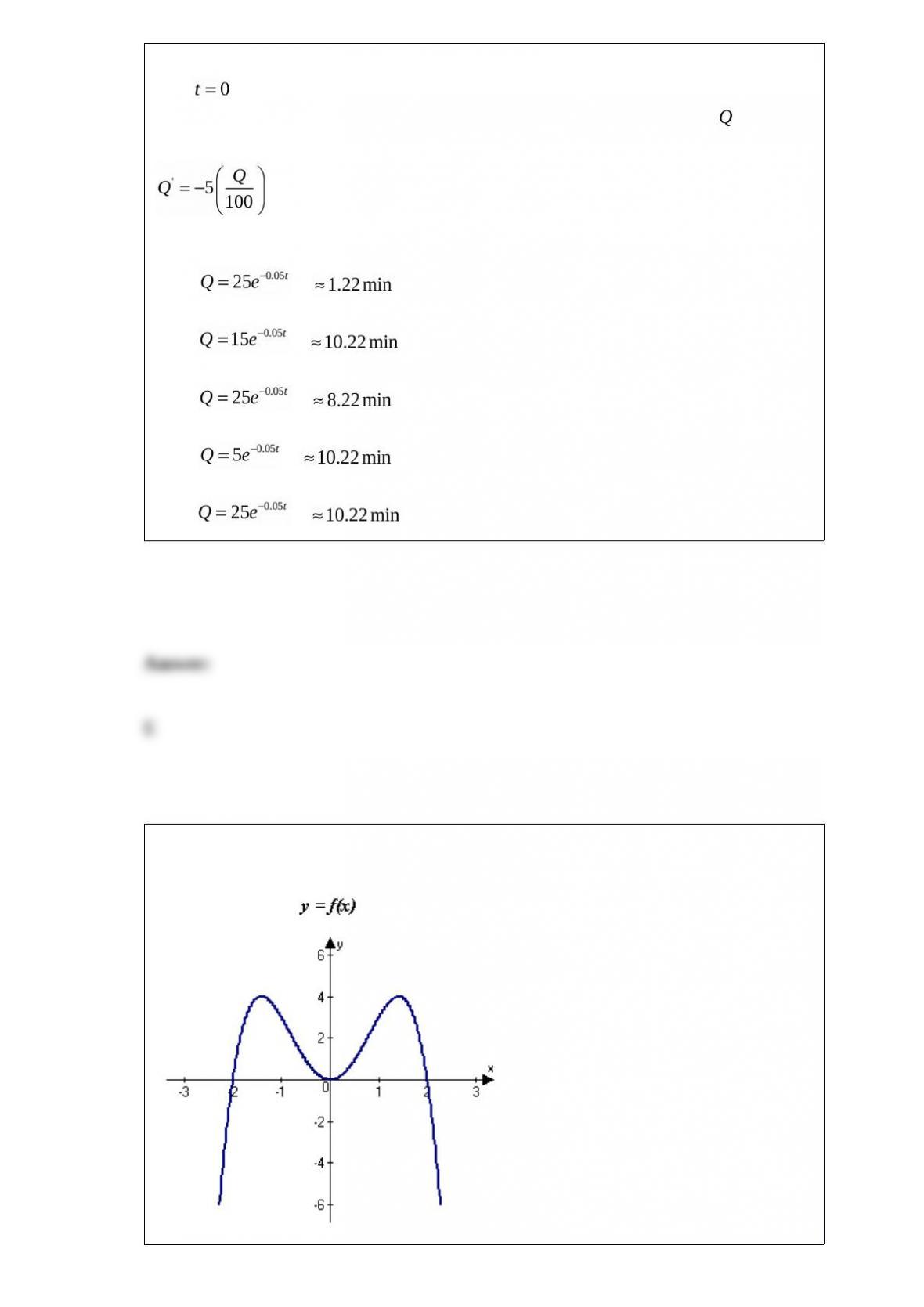
Suppose the number y of medical degrees conferred in the United States can be
modeled by for , where t is the time in
years, with corresponding to 1975. Use the test for increasing and decreasing
functions to estimate the years during which the number of medical degrees is
increasing and the years during which it is decreasing.
A) The number of medical degrees is increasing from 1975 to 1992 and 2000 to 2005,
and decreasing during 1992 to 2000.
B) The number of medical degrees is increasing from 1975 to 1991 and 1999 to 2005,
and decreasing during 1991 to 1999.
C) The number of medical degrees is increasing from 1975 to 1992 and 1999 to 2005,
and decreasing during 1992 to 1999.
D) The number of medical degrees is increasing from 1975 to 1993 and 1999 to 2005,
and decreasing during 1993 to 1999.
E) The number of medical degrees is increasing from 1975 to 1992 and 1998 to 2005,
and decreasing during 1992 to 1998.
Describe the trace of the surface given by the function below in the
xz-plane.
A) circle
B) parabola
C) line
D) ellipse
E) hyperbola
Three people are asked their opinions on a political issue. They can answer “Opposed”
(O) or “Undecided” (U). Find the sample space S.
A)
B)
C)
D)
E)
Use Lagrange multipliers to minimize the function subject to
the following constraint.
Assume that x, y, and z are positive.
A) 81
B) 243
C) 162
D) 486
E) 729
A retail sporting goods store estimates that weekly sales and weekly advertising costs
are related by the equation . The current weekly advertising
costs are $1700, and these costs are increasing at a rate of $130 per week. Find the
current rate of change of weekly sales.
A) 162,500 dollars per week
B) 164,770 dollars per week
C) 87,420 dollars per week
D) 85,150 dollars per week
E) 1,021,570 dollars per week
Find the radius of convergence of the power series.
A)
B) 1
C)
D) -1
E) 0
Find from the given graph.
A)
B)
C)
D)
E)