9
11. A vertical gate keeps water from flowing in a triangular irrigation channel. The channel has a
4-m top width and a 3-m depth. If the channel is full, what is the magnitude of the hydrostatic
force on the triangular gate and its location?
12. A 3-ft square (plane) gate is mounted into an inclined wall (45°). The center of the gate is
located 4 feet (vertically) below the water surface. Determine the magnitude of the
hydrostatic force (in lbs) and its location with respect to the water surface along the incline.
13. A circular gate is installed on a vertical wall as shown in the figure below. Determine the
horizontal force, P, necessary to hold the gate closed if the gate diameter is 6 feet and h = 7
feet. Neglect friction at the pivot.
14. A vertical plate, composed of a square
and a triangle, is submerged so that its
upper edge coincides with the water
surface (Figure P2.5.5). What is the
value of the ratio H/L such that the
pressure force on the square is equal to
the pressure force on the triangle?
15. The wicket dam, pictured on the right, is
5 m high and 3 m wide and is pivoted at
its center. Determine the reaction force
in the supporting member AB.
16. Calculate the magnitude and the location
of the resultant pressure force on the
annular gate shown in the figure to the
right if the cross-section of central hub is
a square that is 1 m by 1 m.
7
17. Determine the relationship between γ1
and γ2 in the figure to the right if the
weightless triangular gate is in
equilibrium in the position shown.
(Hint: Use a unit length for the gate.)
18. An inverted hemispherical shell of
diameter d = 3 feet as shown in the
figure to the right is used to cover a tank
filled with water at 20°C. Determine the
minimum weight the shell needs to be to
hold itself in place (i.e., not be lifted up).
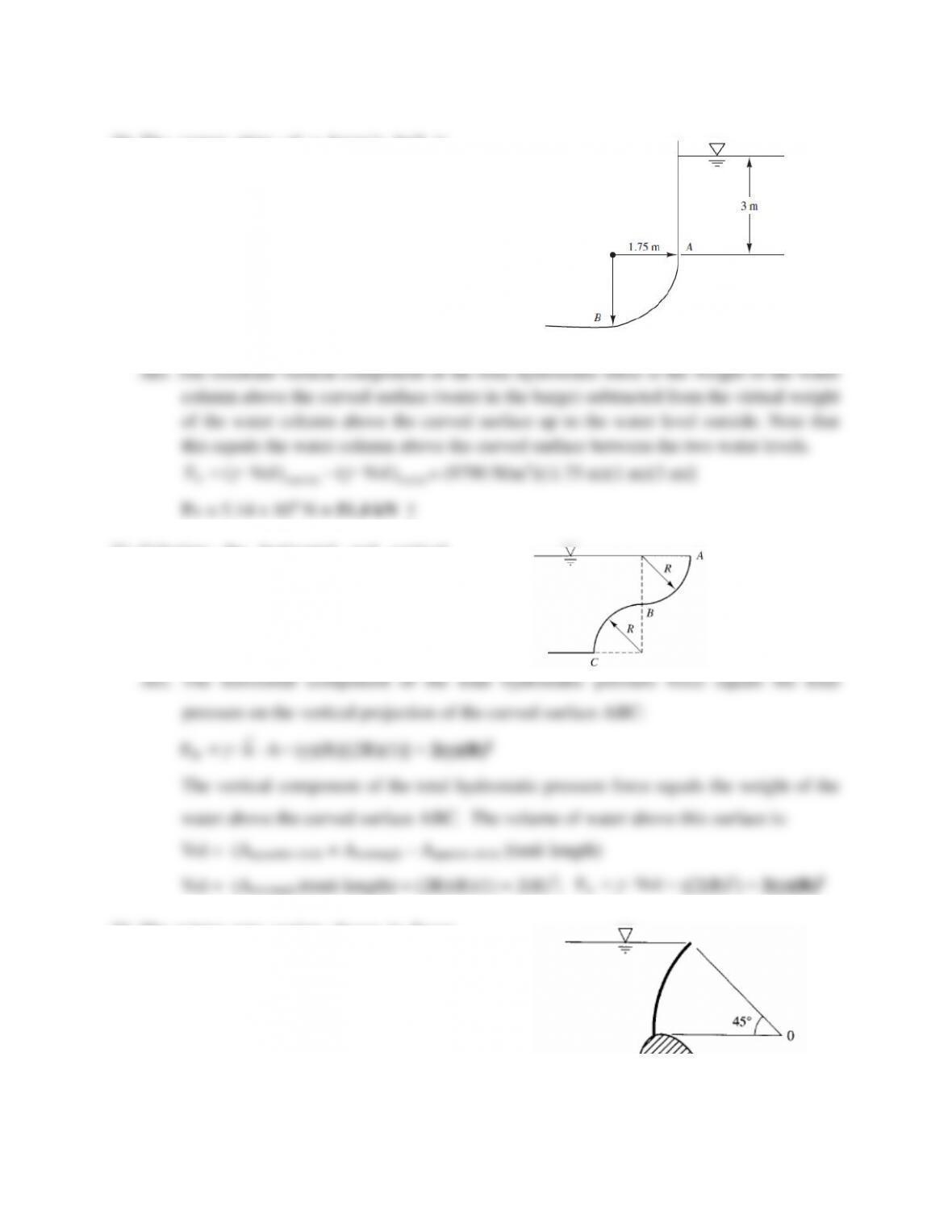
19. The corner plate of a barge’s hull is
curved with a radius of 1.75 m. The
depth of submergence (draft) is depicted
in the figure. However, the barge is
leaking and the water on the inside is up
to level A producing hydrostatic pressure
on the inside as well as the outside.
Determine the resultant horizontal
hydrostatic pressure force on plate AB
per unit length of the hull.
7
20. The corner plate of a barge’s hull is
curved with a radius of 1.75 m. The
depth of submergence (draft) is depicted
in Figure P2.6.4. The barge is leaking
and the water on the inside is up to level
A producing hydrostatic pressure on the
inside as well as the outside. Determine
the resultant vertical hydrostatic force
on plate AB per unit length of hull.
21. Calculate the horizontal and vertical
hydrostatic forces on the curved surface
ABC in the figure to the right.
22. The tainter gate section shown in figure
to the right has a cylindrical surface with
a 12-m radius and is supported by a
structural frame hinged at O. The gate is
10 m long (in the direction perpendicular
to the page). Determine the magnitude,
direction, and location of the total
hydrostatic force on the gate
7
23. A piece of irregularly shaped metal weighs 301 N. When the metal is completely submerged
in water, it weighs 253 N. Determine the specific weight and the specific gravity of the
metal.
24. A concrete block that has a total volume of 12 ft3 and a specific gravity of 2.67 is tied to one
end of a long cylindrical buoy as depicted in the figure below. The buoy is 10 ft long and is
2 ft in diameter. Unfortunately the water level has risen and the buoy is floating away with 1
ft sticking above the water surface. Determine the specific gravity of the buoy. The fluid is
brackish bay water (S.G. = 1.02).
8
25. A cube of ice measures 10 inches on each side. It has a density of 1.76 slugs/ft3. Determine
the weight of the ice and the percentage of the cube below the waterline when it is floating.
26. A rectangular barge is 14 m long, 6 m wide, and 2 m deep. The center of gravity is 1.0 m
from the bottom and the barge drafts 1.5 m of seawater (S.G. = 1.03). Find the metacentric
height and the righting moments for a 8° angle of heel (or list).